This post is based on my recent talk "Trust-by-Design for AI Developer Tools" and summarizes a practical approach to building trustworthy AI systems for developers. We start with how mathematics sought trust-by-design through axioms and proofs, face the reality brought by Gödel’s theorems, and then pivot to architectures that deliver reliability from unreliable components — a mindset crucial for modern AI tooling.
How to Build Trust?
Long before software, mathematics pursued trust-by-design via explicit assumptions. Euclid’s
postulates built an entire universe of geometry in his book Elements;
centuries later, Hilbert aimed for a formal system
that’s complete, consistent, and decidable. These were early trust engines.
Euclid’s Elements proved so influential that it became the second
most widely read book (after the Bible) for over 2000 years!
The success of Euclid’s axiomatic method cemented the idea that certainty
in knowledge could be constructed from a small foundation of trusted assumptions.

Hilbert epitomized this optimism in the early 20th century, believing that through a complete and consistent set of axioms, all of mathematics could be resolved with absolute rigor. He famously declared “We must know – we will know!”, a bold proclamation (later inscribed on his tombstone) reflecting his conviction that every well-posed mathematical problem is solvable in principle. Hilbert’s program sought to eliminate doubt by proving mathematics internally consistent and complete.

A Cold Shower from Gödel
In 1931, Kurt Gödel shattered Hilbert’s dream by proving that any sufficiently expressive formal system can’t be both complete and self-certifying for consistency. In simple terms he showed that there is no single switch of trust — we need layers: external meta-checks, independent evaluations, and architectures that detect issues and roll back safely. This revelation was a shock to mathematicians and logicians worldwide. It meant no single set of axioms could serve as the ultimate foundation of truth – any formal system rich enough to express arithmetic would inevitably contain true statements unprovable within the system, and it could not prove its own consistency.
The implications went beyond mathematics. If absolute certainty was unattainable even in arithmetic,
then complex real-world systems would also require external checks and balances.
Gödel’s personal story also is tragically notable: despite his towering intellectual achievements,
he struggled with severe anxiety and paranoia. Near the end of his life in Princeton,
he would only eat food prepared by his wife Adele, fearing poisoning; when she was hospitalized
and unable to care for him, Gödel refused to eat and tragically died from self-starvation.
At the same time, calling it “madness” is misleading – his professional reasoning remained
extraordinarily sharp for decades despite his illness.
Gödel’s legacy is the combination of genius and human fragility.
Importantly, his incompleteness theorems taught science and engineering that
layered trust is not optional, but a necessity.

Then How to Build Trust?
John von Neumann, in a 1952 lecture, showed how to synthesize reliable organisms from unreliable components. In essence, he proved that with clever architecture (like redundancy and error-correction),
a system made of fallible parts can still deliver very high reliability. This idea — reliability through structure — became a roadmap for modern AI tools: define clear contracts, implement layered checks, and perform meta-level audits on the system’s behavior.
In practice, that means no single component is trusted absolutely; each layer is monitored or constrained by another,
ensuring that faults can be caught and mitigated at different levels.

Beyond structural architecture, mathematics and computer science also introduce probabilistic methods to build trust under uncertainty. For instance, Bayes’ theorem (1763) gives a mathematical rule for updating the probability of a hypothesis given new evidence. In other words, it tells us how much to trust a new piece of data in light of what we already believe, which is why it has been nicknamed an “evidence trust formula”. Bayesian inference allows an AI system to continuously update its confidence as more observations arrive – a crucial aspect of trusted decision-making in domains where no prediction is 100% certain.
In a more modern vein, Leslie Valiant’s Probably Approximately Correct (PAC) learning framework (1984) formalized the idea that if an algorithm sees enough representative data, it will “probably” learn an “approximately correct”. PAC theory provides explicit bounds on the likelihood that a learned model will perform well, offering a theoretical guarantee of reliability within quantifiable probability limits.
Similarly, in information theory, Claude Shannon proved in 1948 that by encoding messages with appropriate redundancy, one can achieve essentially error-free communication over a noisy channel. This result assured engineers that reliability can emerge even in noisy, uncertain environments by design. Across these advances, the theme is consistent: when absolute certainty is unattainable, we can still pursue quantified trust – building systems that have provable limits on their error rates and mechanisms to keep those errors in check.

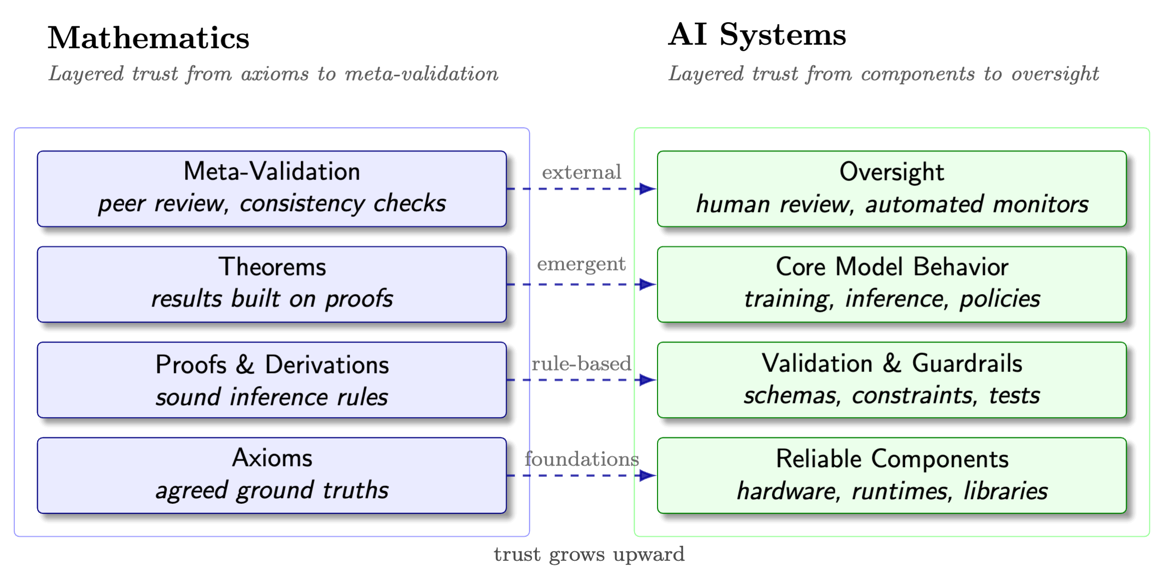
To visualize consider how both mathematics and AI rely on
layered trust architectures. In mathematics,
we start from foundational axioms, build up through proofs to theorems,
and then often invoke external consistency checks
(peer review, meta-mathematical validation) at the highest level.
In AI systems, we begin with reliable low-level components, add layers of validation
(data schemas, constraints, guardrails) around a core model,
and finally apply oversight – for example, human review or automated monitors that can
catch and correct mistakes. The diagram below compares these structures side-by-side.
JetBrains’ Way: Trust-by-Design in Dev Tools
Trust for developers starts with the IDE — solid defaults, static analysis, and type-aware tooling — and extends to AI assistants. The same interface now hosts an autonomous coding agent that must be auditable and controllable: suggestions are visible, testable, and the developer retains final responsibility. In essence, the development environment itself implements many of the layered trust principles described above: the AI’s suggestions are checked against coding standards and tests, and ultimately a human developer vets the changes.
Takeaways
- Trust isn’t a binary switch; it’s a stack of verifications across data, models, and deploy. For us trust is also a process when we are getting to know something and adapting to the new tools, for instance.
- Architect reliability from the outset: contracts, guardrails, telemetry, and rollbacks.
- Keep the developer in control: transparency, testability, and clear code.