Mini-Research at Home: Soccer Ball

Almost everyone has a soccer ball at home, stitched together from polygons. If you look closely at its surface, at each vertex exactly three faces meet, and every face is always one of two types: a regular pentagon or a regular hexagon.

Soccer Ball

Method 1: via curvature and the Gauss–Bonnet theorem

In the plane, the ideal angle sum around a vertex for hexagons is

which gives zero angular defect and curvature $0$ (this is the hexagonal lattice — like honeycombs or graphene).

Honeycombs and Graphene

On the sphere, the sum must be less than $360^\circ$, i.e. there must be a positive angular defect. Replacing one hexagon with a pentagon decreases the total angle by $60^\circ$, introducing a defect of $ +\frac{\pi}{3}$.
Indeed, the interior angle of a regular pentagon is $ \pi - \frac{2\pi}{5} = \frac{3\pi}{5} = 108^\circ$, which is exactly $12^\circ$ less than $120^\circ$. For all five angles that gives $ 5 \times 12^\circ = 60^\circ = \frac{\pi}{3}$.

It is known that the total Gaussian curvature of a sphere equals $4\pi$ (Gauss–Bonnet theorem). Thus, to account for all curvature we need exactly $$ \frac{4\pi}{\pi/3} = 12 $$ pentagons.

Gauss–Bonnet theorem

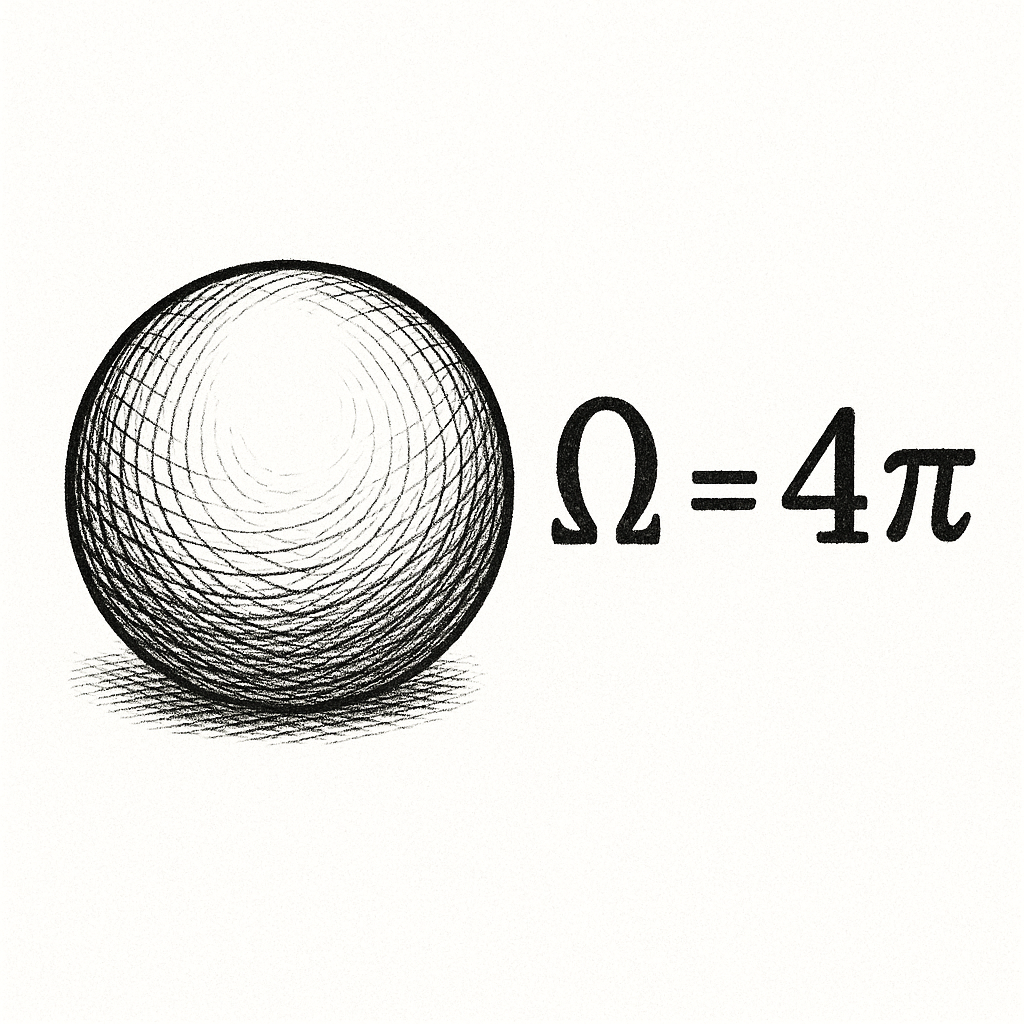
This gives the famous rule: any “spherical” hexagonal network must contain exactly 12 pentagonal defects. Such polyhedra are also called fullerenes $C_n$, where $n$ is the number of vertices. These are real molecular compounds consisting of three-coordinated carbon atoms; it was first generated in 1984 by Eric Rohlfing, Donald Cox, and Andrew Kaldorthe, and it got the Breakthrough of the Year Award 1991 for the most significant development in scientific research! The classical soccer ball in essence is the fullerene $C_{60}$, consisting precisely of 12 pentagons and 20 hexagons. Since at each vertex exactly three faces meet, the number of edges counted with repetitions $$ 5 \cdot 12 + 6 \cdot 20 = 3 \cdot 60 $$ is satisfied. If we "slice" the ball into layers, there are six:

1 pentagon
5 hexagons
10 polygons (5 pentagons + 5 hexagons)
10 polygons (5 pentagons + 5 hexagons)
5 hexagons
1 pentagon (opposite to the first)

Method 2: via Euler’s formula

Let us denote:

• $P$ — the number of pentagons,
• $H$ — the number of hexagons,
• $F = P+H$ — the total number of faces,
• $E$ — the number of edges,
• $V$ — the number of vertices.

For the classical ball, three edges meet at each vertex, hence $$ 3V = 2E $$ (since each edge is counted twice, once from each endpoint).

On the other hand, the sum of polygon sides is $$ 5P + 6H = 2E $$ (since each edge belongs to two faces). Euler’s formula for the sphere:

Substitute $V = \tfrac{2E}{3}$, $F = P+H$: $$ \frac{2}{3}E - E + (P+H) = 2, $$ which simplifies to $$ E = 3(P+H-2). $$ Return to the side count: $$ 5P + 6H = 2E = 6(P+H-2) = 6P + 6H - 12. $$ Thus, $$ 5P + 6H = 6P + 6H - 12 \quad \Rightarrow \quad P = 12. $$ So there are always 12 pentagons, regardless of how many hexagons!

For the soccer ball case, if $V=60$, then $E=90$. Now compute $H$: $$ 5 \cdot 12 + 6H = 2E = 180 \quad \Rightarrow \quad 60 + 6H = 180 \quad \Rightarrow \quad H=20. $$

Generalization of the 12 Pentagons Rule

Let's call a convex polyhedron simple if exactly 3 edges meet at each vertex. Then we can prove a more general fact: for any simple polyhedron, the following formula holds:

from which we can see that faces with fewer than 6 sides always "lack" exactly 12 units of curvature. In the particular case of fullerenes (where $p_3=p_4=0$ and $p_k=0$ for $k\ge7$) it reduces to $p_5=12$.

Connection between Euler's Theorem and Curvature

As we can easily sense from the two methods of reasoning above, these are two sides of the same mathematical coin. Euler's theorem ($V - E + F = 2$ for a spherical polyhedron) is closely related to the distribution of curvature on the surface.
In each convex polyhedron, the deficit of angles at vertices (that angular defect $\delta$) sums to a constant value. Descartes' theorem (a special case of the Gauss-Bonnet theorem for polyhedra) states that the sum of all angular defects on a closed surface, topologically equivalent to a sphere, equals $4\pi$ radians (or $720^\circ$). See: Descartes' theorem.
In other words, for any convex polyhedron $$\sum\limits_{v \in V}\delta(v) = 720^\circ.$$ This fact can be understood by splitting the polyhedron surface into pyramids around each vertex: the total angle at the base of pyramids is $360^\circ$ per vertex, and the sum of face angles at this vertex is less than $360^\circ$ by the amount the vertex is "bent" (curvature is concentrated at vertices). Adding defects of all vertices, we account for a full circular rotation around each, and the total "excess" to planar development gives $720^\circ = 4\pi$ for a sphere. See: Euler characteristic.
For a two-dimensional polygon, we all did a similar exercise in school, getting the sum of angular defects equal to $360^\circ = 2\pi$.
It's important that the Euler characteristic of a surface is related to the total curvature. In general form, the Gauss-Bonnet theorem states that for a compact surface without boundary $$ \int KdA + \sum\limits_{v \in V} \delta(v)=2\pi\chi, $$ where $K$ is Gaussian curvature (for a polyhedron it's concentrated at vertices, so the integral over faces is zero) and $\chi$ is the Euler characteristic. See: Gauss-Bonnet theorem.
For a sphere $\chi=2$, therefore $2\pi\chi = 4\pi$ and we get Descartes' formula mentioned above.
For example, for a torus $\chi=0$, and indeed the total angular defect equals $0$ – in a polyhedron with torus topology, positive and negative curvature are distributed so that they mutually compensate.
So Euler's formula and the Gauss-Bonnet theorem are essentially two faces of the same truth: the combinatorics of a grid on a surface is related to the total curvature of that surface. If all vertices are "identical" (as in the case of uniform polyhedra), then from the sum of defects $720^\circ$ we immediately derive the number of vertices: $V = 720^\circ / \delta$.
For example, for an icosahedron each vertex has a defect of $360^\circ - 5\cdot 60^\circ = 60^\circ$, and we get $720^\circ/60^\circ = 12$ vertices. Thus, the topological Euler formula transforms into the geometric theorem about curvature sum, and conversely – by considering curvature (defects), we can derive constraints on the structure of polyhedra and graphs on surfaces.

Open Problem: Polyhedron without Diagonals

Is there a polyhedron (not necessarily convex) where each pair of vertices is connected by an edge? In other words, can we realize the complete graph $K_n$ in a three-dimensional polyhedron without self-intersections for $n>4$?