Introduction
For several years now, I’ve been preparing a team from Neapolis University Pafos (Cyprus)
and serving on the Jury of the International Mathematics Competition (IMC) for university students.
Naturally in parallel, it’s also fascinating to follow, the progress of LLMs (Large Language Models) in solving extremely
difficult Olympiad-level math problems. Beyond its scientific significance,
mathematics also serve as a nearly universal system for testing intellectual ability in children:
in almost every country, a mathematics exam is a mandatory requirement for university admission.
The advantages are obvious: problems of varying difficulty can be solved quickly using pen and paper,
and the grading criteria are relatively objective.
A bit of History
Three years ago, even the most advanced models couldn’t solve anything from the IMC,
although the first public version of ChatGPT (based on GPT‑3.5, released by OpenAI on November 30, 2022)
could already handle simpler math problems.
In January 2024, Google DeepMind published AlphaGeometry
a specialized system with Reinforcement Learning and Symbolic Deduction focused on solving
high school-level geometry problems from the IMO (International Mathematical Olympiad).
A year later, in January 2025, another specialized system LIPS
appeared, designed to tackle challenging Olympiad-style inequalities —
and also general-purpose LLMs kept getting smarter too.
Then recently came two major announcements in July 2025, just two days apart:
both OpenAI
and Google DeepMind
models had achieved gold medal performance at the IMO level!
Reading the news about all this is one thing —
but testing the current capabilities of the strongest publicly
available models firsthand is something else entirely.
Fair Experimental Setup
This experiment will benchmark state-of-the-art LLMs
on university-level math Olympiad problems
from the IMC-2025.
The goal is to assess each model's reasoning capabilities and problem-solving performance
under conditions similar to the human competition.
We presented the same 10 problems (5 per round, 2 rounds) to each model
and evaluated their solutions rigorously. As at real IMC,
together with Andrei Smolensky,
who has also been participating in the work of the IMC Jury for a few years,
we perform checking and adjusting the final mark for each problem
after discussion between the judges.
By mimicking contest conditions (no prior exposure to the problems,
independent work), we aim to see how close these models
come to human-level performance on challenging math problems.
To ensure the results are comparable and unbiased,
we carefully controlled the experimental setup and created a Python script for solution generation.
The script is available on GitHub.
- We provided each problem in a clear LaTeX format. This guarantees all models can read the problem easily. Each model receives the problem via an identical prompt structure.
- We used a system message to prime the model with general problem-solving instructions and a user message containing the problem statement. This two-part prompt (detailed in the script above) is the same for GPT, DeepSeek, Gemini, Claude, and Grok tailored only as needed to fit each platform's format.
- We run each reasoning model 3 times, and then ask the same model to read through all 3 solution variants and come up with the final version. Sometimes we got only 2 variants, or even 1 due to the token limits for thinking, but to be honest, even at real IMC, some solutions occasionally get lost at the beginning and are only checked later during the appeals process. We marked all the solution variants and set the maximum score among all solutions. At a real IMC, usually only one solution in the final version is checked at first, but often team leaders come to the appeal with drafts and explanations, from which a more complete solution to the problem can be assembled =)
- We allow the models to perform multi-step reasoning or use tools (like a scratchpad, calculator, or code execution) to solve problems, but we ask them not to use internet search. All models run in a single-turn (single prompt) setting – meaning we present the problem and the model must produce a solution in one go, possibly with internal chain-of-thought, but without any further user feedback.
- Each problem is given in a fresh session and context for the model, so it has no memory of other problems or its own previous answers. This prevents any carry-over of information.
Problem Example
Problem 2, First Day. Let $f:\mathbb{R}\to\mathbb{R}$ be a twice continuously differentiable function, and suppose that
Prove that
You can look at all ten problems here or on the official IMC-2025 page.
IMC-2025 AI team Result
| Model | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 | Sum |
|---|---|---|---|---|---|---|---|---|---|---|---|
| gemini-2.5-pro | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 100 |
| o3-2025-04-16 | 10 | 10 | 10 | 10 | 10 | 10 | 3 | 10 | 10 | 10 | 93 |
| claude-opus-4-20250514 | 10 | 2 | 10 | 1 | 10 | 10 | 0 | 10 | 10 | 2 | 65 |
| grok-4 | 10 | 10 | 10 | 1 | 8 | 10 | 2 | 10 | 1 | 2 | 64 |
| deepseek-R1-0528 | 10 | 2 | 10 | 1 | 10 | 10 | 0 | 8 | 1 | - | 52 |

Conclusion
Summer 2025 for Olympiad Mathematics is obviously analogous
to Spring 1997 for Chess and Spring 2016 for Go:
from now on, even the best humans cannot outperform AI
in the highly specialized solution of Olympiad Mathematics problems.
In recent years, it has been clear that this moment would inevitably come,
but for some reason I still personally feel a little sad that this milestone has fallen.
We can rejoice in the new possibilities that such tools open up for us,
exploring new depths and discovering new facets of mathematics with their help.
Some takeaways
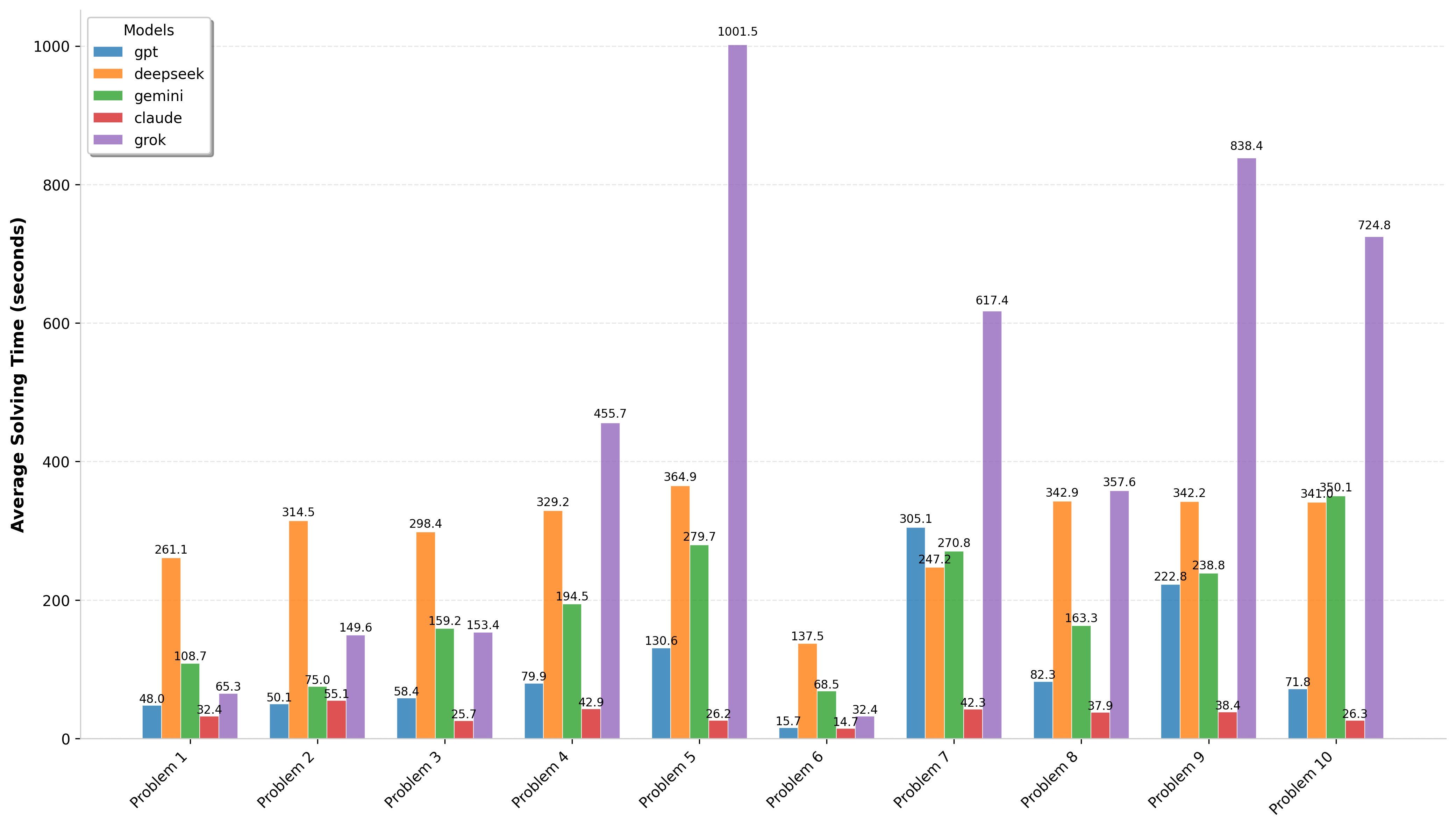
- It was fascinating to read DeepSeek’s thought process while solving the problems.
- DeepSeek thinks a lot and for a long time, which actually hinders it on olympiad-style problems.
- Gemini writes very clearly and reasonably, but despite this for problem 7, for example, only its second attempt was correct.
- The hardest problems for LLMs were #4, #7, and #10 — they don’t rely on a single clever idea, but rather require multiple steps and deeper reasoning.
- Overall, checking AI solutions feels eerily similar to grading students' work..
- Even though I asked not to use the internet search via the system prompt, I'm not sure that all LLMs listened =) What's more, on the contrary, I'm sure that some of them used the search, but at the same time I'm also sure that we owe the main advances and final scores to the increasingly "smarter" LLMs, and not to simple cheating.
- Such a simple Python script and a few API keys find solutions to even very complex problems.

A bit of self-promotion
From time to time I plan to write similar thoughts in the Telegram channel @TechneNotes, so join me if you liked it.