nup_logo

Fundamentals of Machine Learning

Recurrent neural networks basics


Alex Avdiushenko
November 12, 2024

Disadvantages of Feed-Forward (and also Convolutional) Neural Networks

Or why we need recurrent ones :)

  • The input is only fixed-dimensional vectors (e.g., 28×28 images)
  • The output is also a fixed dimension (for example, probabilities of 1000 classes)
  • Fixed number of computational steps (i.e., network architecture)

A. Karpathy. The Unreasonable Effectiveness of Recurrent Neural Networks

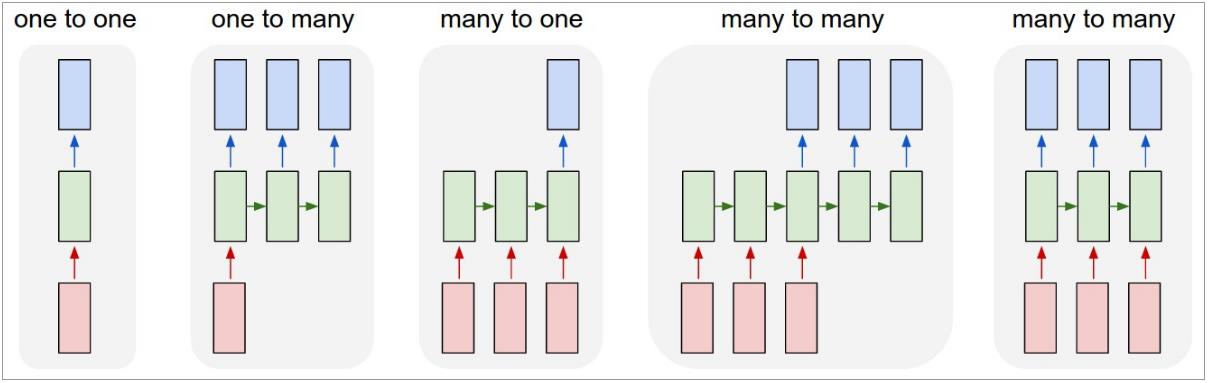
RNN Architectures

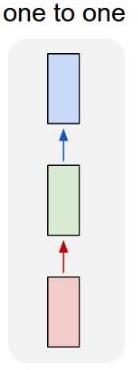
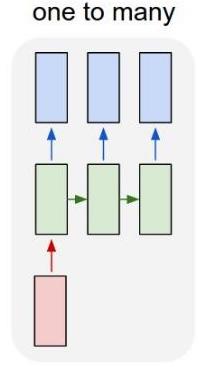
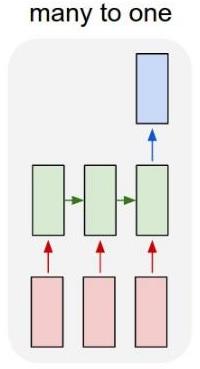
Architectures of Recurrent Networks

One-to-One Architecture One-to-Many Architecture
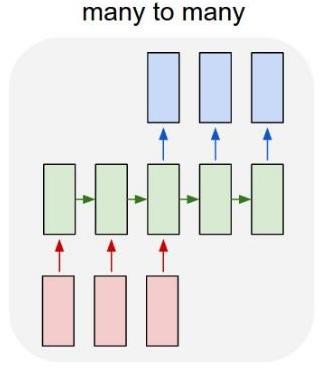
Vanilla Neural Networks Image Captioning
image → (sequence of words)
Many-to-One Architecture Many-to-Many Architecture
Sentiment Classification
(sequence of words) → sentiment		 Machine Translation
(seq of words) → (seq of words)
Many-to-Many Architecture 2

Video Classification

(on frame level)

Sequential Processing of Fixed Input

Sequential Processing

J. Ba, V. Mnih, K. Kavukcuoglu. Multiple Object Recognition with Visual Attention

Sequential Generation of Fixed Output

Sequential Generation

K. Gregor, I. Danihelka, A. Graves, D. J. Rezende, D. Wierstra.
DRAW: A Recurrent Neural Network For Image Generation

Recurrent Neural Network scheme

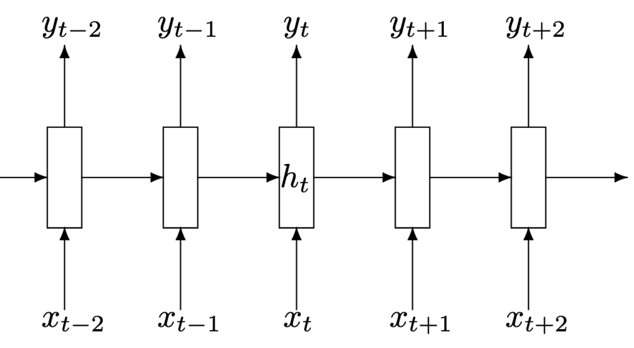
rnn_scheme

Recurrent Neural Network

We process the sequence of vectors $x$ with one and the same function with parameters:

$$ h_t = f_W(h_{t-1}, x_t)$$

$f_W$ is a function parameterized by $W$

$x_t$ — next input vector

$h_t$ — hidden state

Question: What function can we take as $f_W$?

Vanilla Recurrent Neural Network

$$ h_t = f_W(h_{t-1}, x_t)$$

As a function $f_W$ we set a linear transformation with a non-linear component-wise "sigmoid":

$$ \begin{align*} h_t &= \tanh ({\color{orange}W_{hh}} h_{t-1} + {\color{orange}W_{xh}} x_t) \\ y_t &= {\color{orange}W_{hy}} h_t \end{align*} $$

Character Level Model Example

The entire four-letter dictionary: [h, e, l, o] and word "hello" as train:

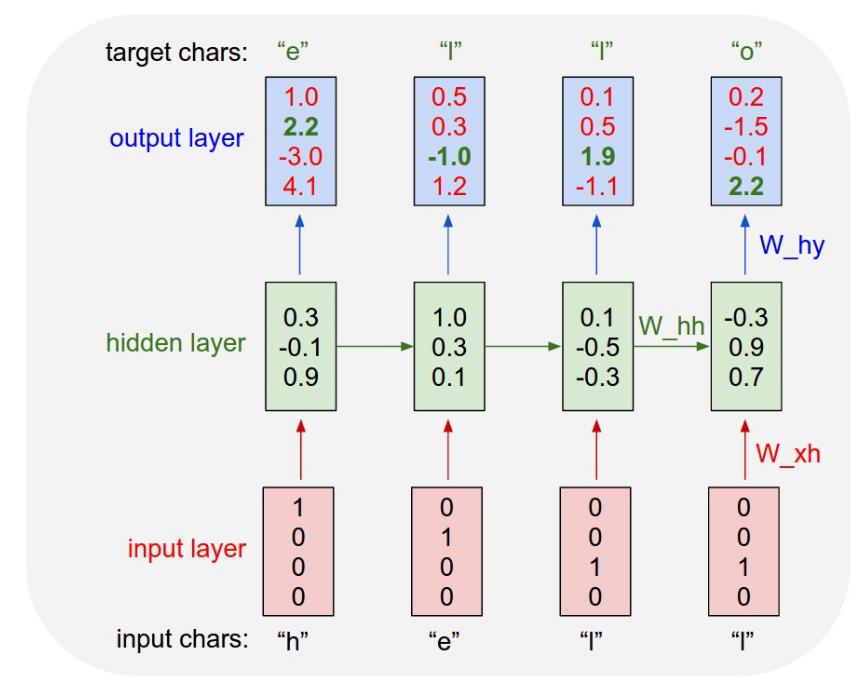
Character Level Model Example

Softmax is also applied to the values of the out-layer to get the loss

Demo

numpy implementation by Karpathy



Let's get to grips with the code in the Jupyter notebook!

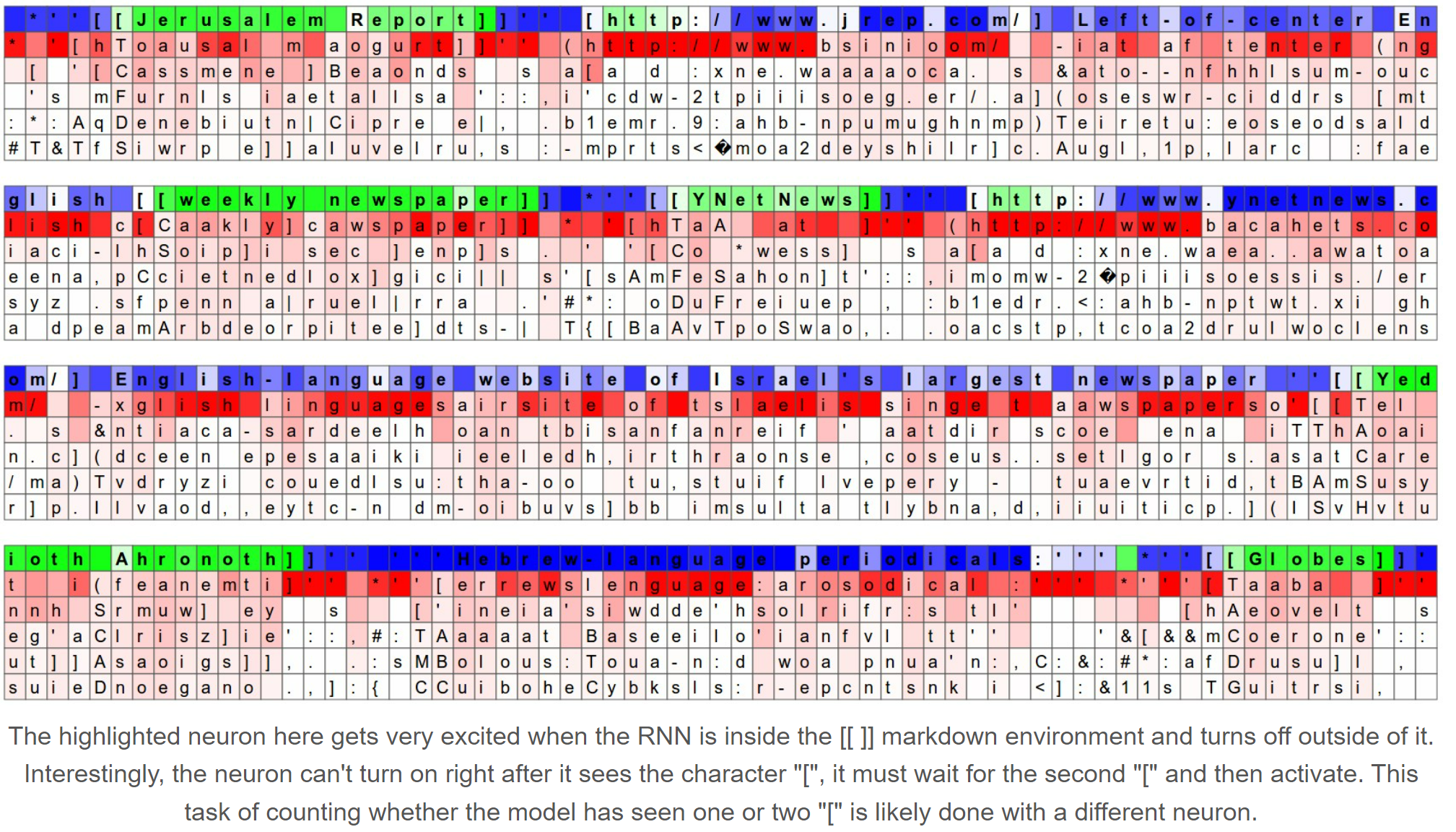
How does it work?

Neuron Analysis
Bracket Neuron
Cell Endline

Deep Recurrent Networks



$$ \quad h_t^\ell = \tanh {\color{orange}W^\ell} \left(\begin{array}{c} h_t^{\ell-1} \\ h_{t-1}^{\ell} \end{array}\right) $$ $$ \quad h \in \mathbb{R}^n, \quad {\color{orange}W^\ell} [n \times 2n] $$
Deep RNN
Question: What is the main problem with vanilla RNN?

Long short-term memory (LSTM)

$$ \begin{align*} &{\color{orange}W^\ell} [4n\times 2n] \\ \left(\begin{array}{c} i \\ f \\ o \\ c_t^\prime \end{array}\right) &= \left(\begin{array}{c} \text{sigm} \\ \text{sigm} \\ \text{sigm} \\ \tanh \end{array}\right) {\color{orange}W^\ell} \left(\begin{array}{c} h_t^{\ell-1} \\ h_{t-1}^{\ell} \end{array}\right) \\ &\begin{array}{l} c_t^\ell = f \odot c_{t-1}^\ell + i \odot c_t^\prime \\ h_t^\ell = o \odot \tanh(c_t^\ell) \end{array} \end{align*} $$

$\odot$ — component-wise product

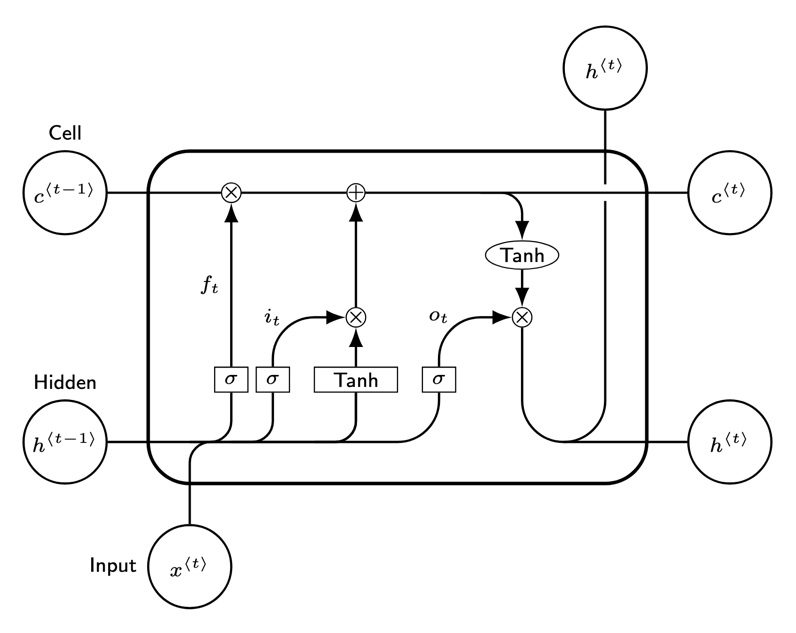
LSTM: Motivation and Schema

The network should remember the context for a long time. Which context? The network learns itself. To do this, the vector \(c_t\) is introduced, which is the state vector of the network at the moment \(t\).

\(c_t^\prime = \tanh({\color{orange}W_{xc}}x_t + {\color{orange}W_{hc}}h_{t-1} + {\color{orange}b_{c^\prime}})\) candidate cell state
\(i_t = \sigma({\color{orange}W_{xi}}x_t + {\color{orange}W_{hi}}h_{t-1} + {\color{orange}b_{i}})\) input gate
\(f_t = \sigma({\color{orange}W_{xf}}x_t + {\color{orange}W_{hf}}h_{t-1} + {\color{orange}b_{f}})\) forget gate
\(o_t = \sigma({\color{orange}W_{xo}}x_t + {\color{orange}W_{ho}}h_{t-1} + {\color{orange}b_{o}})\) output gate
\(c_t = f_t \odot c_{t-1} + i_t \odot c_t^\prime\) cell state
\(h_t = o_t \odot \tanh(c_t)\) block output
lstm_scheme

GRU: Gated Recurrent Unit

$$ \begin{align*} u_t &= \sigma({\color{orange}W_{xu}}x_t + {\color{orange}W_{hu}}h_{t-1} + {\color{orange}b_{u}}) \\ r_t &= \sigma({\color{orange}W_{xr}}x_t + {\color{orange}W_{hr}}h_{t-1} + {\color{orange}b_{r}}) \\ h_t^\prime &= \tanh({\color{orange}W_{xh^\prime}}x_t + {\color{orange}W_{hh^\prime}}(r_t\odot h_{t-1})) \\ h_t &= (1-u_t) \odot h_t^\prime + u_t \odot h_{t-1} \end{align*} $$

Only \( h_t \) is used, vector \( c_t \) is not introduced. Update-gate instead of input and forget. The reset gate determines how much memory to move forward from the previous step.

Disadvantages of Vanilla RNN

$$ h_t = f_W(h_{t-1}, x_t)$$

As a function \( f_W \) we set a linear transformation with a non-linear component-wise "sigmoid":

$$ \begin{align*} h_t &= \tanh ({\color{orange}W_{hh}} h_{t-1} + {\color{orange}W_{xh}} x_t) \\ y_t &= {\color{orange}W_{hy}} h_t \end{align*} $$

Disadvantages

  • Input and output signal lengths must match
  • "Reads" the input only from left to right, does not look ahead
  • Therefore, it is not suitable for machine translation, question answering tasks, and others

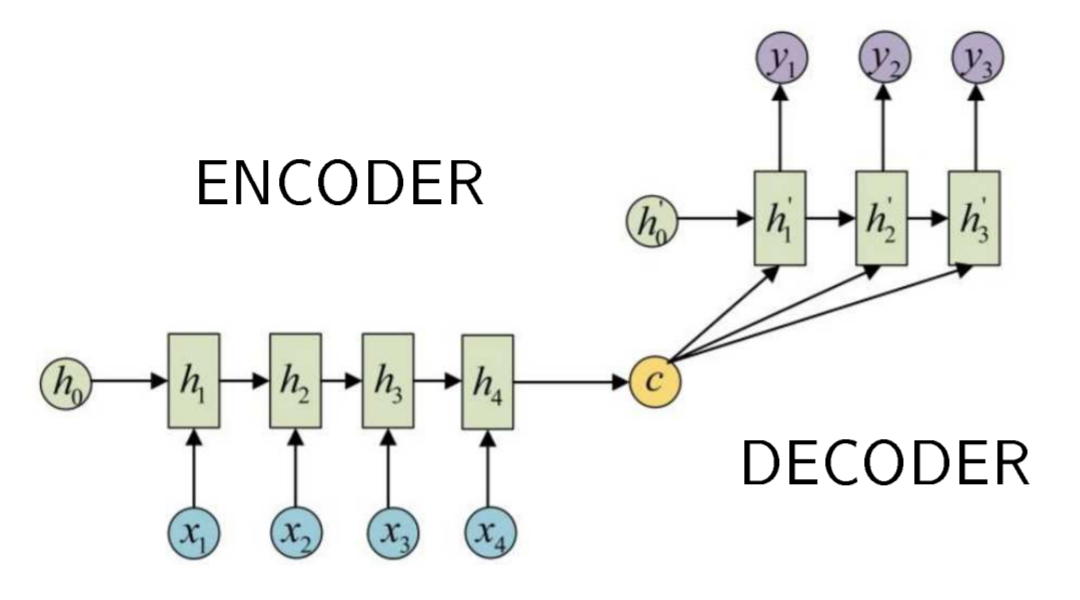
RNN for sequence synthesis (seq2seq)

\(X = (x_1, \dots, x_n)\) — input sequence

\(Y = (y_1, \dots, y_m)\) — output sequence

\(\color{green}c \equiv h_n\) encodes all information about \(X\) to synthesize \(Y\)

Sequence to Sequence Model
$$ \begin{align*} h_i &= f_{in}(x_i, h_{i-1}) \\ {\color{green}h_t^\prime} &{\color{green}= f_{out}(h_{t-1}^\prime,y_{t-1},c)} \\ y_t &= f_{y}(h_t^\prime, y_{t-1}) \end{align*} $$

Summary

  • Recurrent neural networks — a simple, powerful, and flexible approach to solving various machine learning problems
  • Vanilla RNNs are simple, but still not good enough
  • So you need to use LSTM or GRU, and seq2seq architecture
  • LSTM prevents zeroing gradients
  • Clipping helps with "explosion of gradients" as usual
  • We need a deeper understanding, both theoretical and practical — there are many open questions

What else can you look at?