
Fundamentals of Machine Learning
Convolutional neural networks
Alex Avdiushenko
November 26, 2024

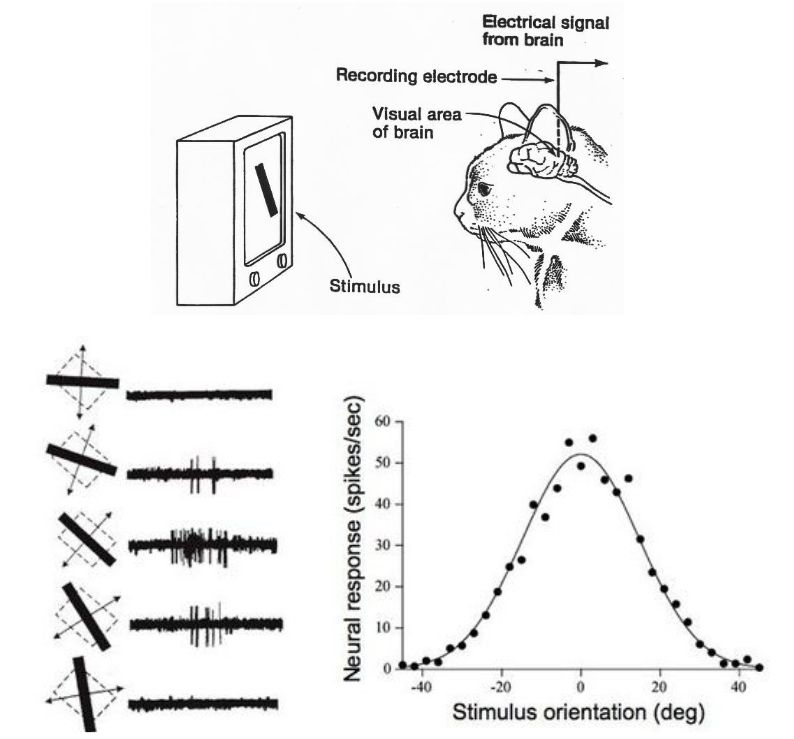
Hubel & Wiesel (1959)
History
The Nobel Prize in Physiology or Medicine, 1981
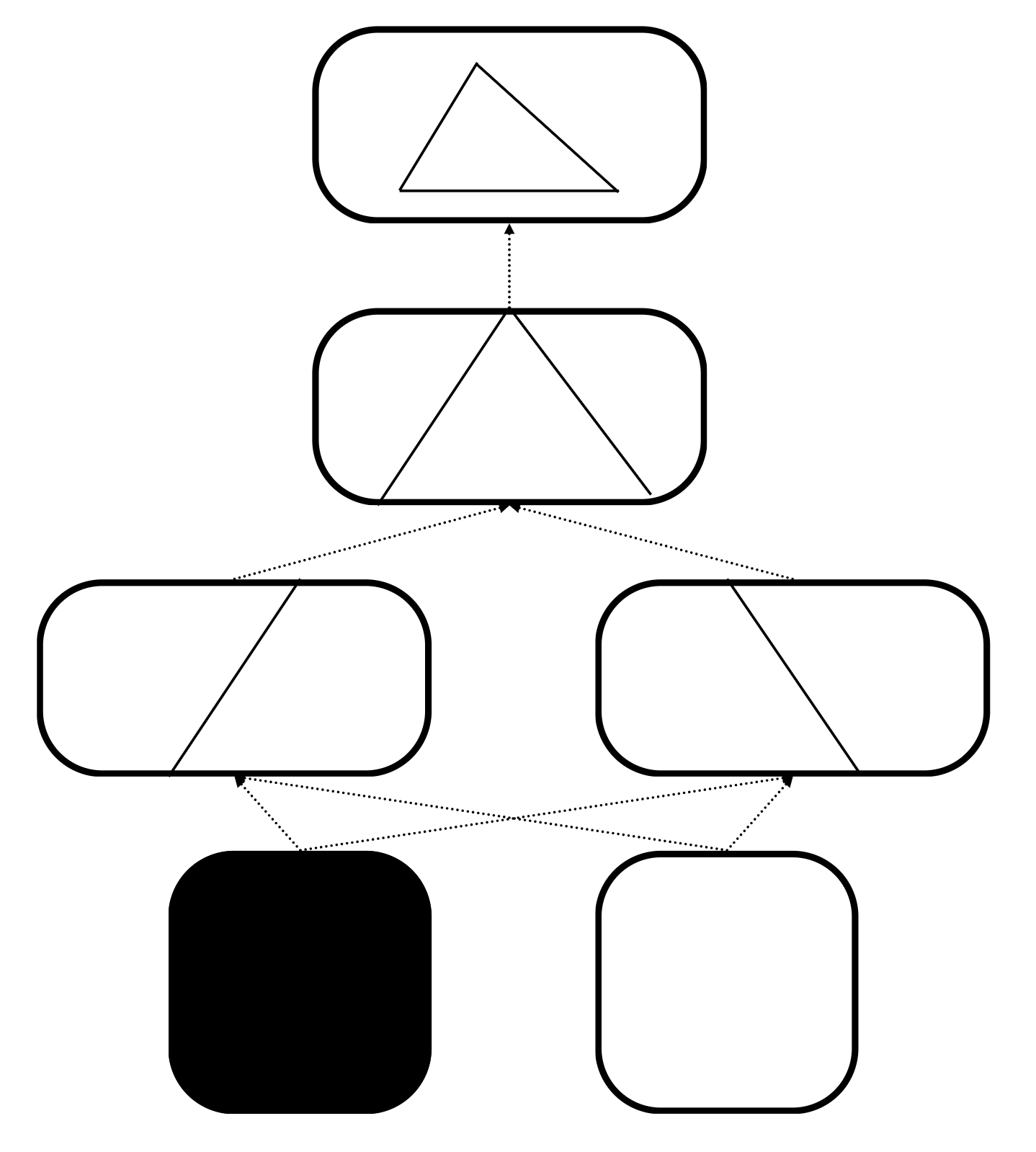
Fukushima (1980)
History
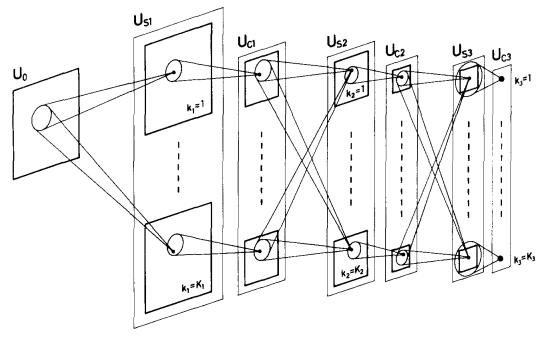
Convolutions and activations have already been used, but without gradient descent optimization and supervised learning
LeCun, Bottou, Bengio, Haffner (1998)
First success
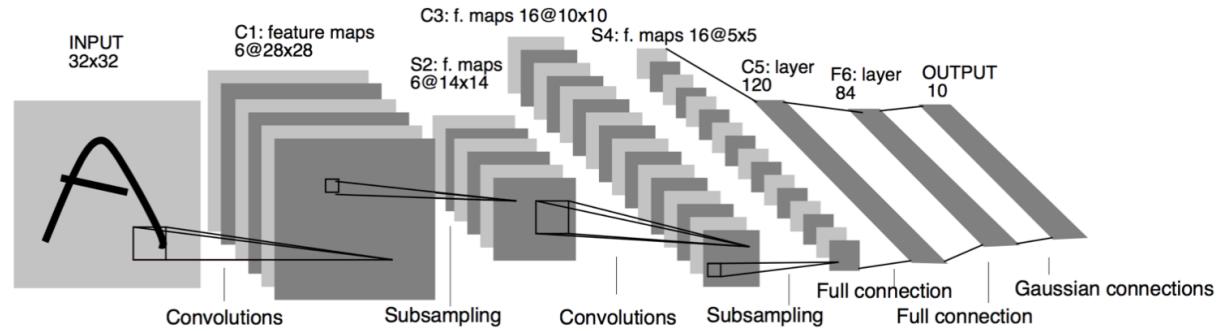
Note: Then quite good results were obtained using the LeNet architecture.
Krizhevsky, Sutskever, Hinton (2012)
A real breakthrough
The Winner of the ImageNet contest of the 2012 year
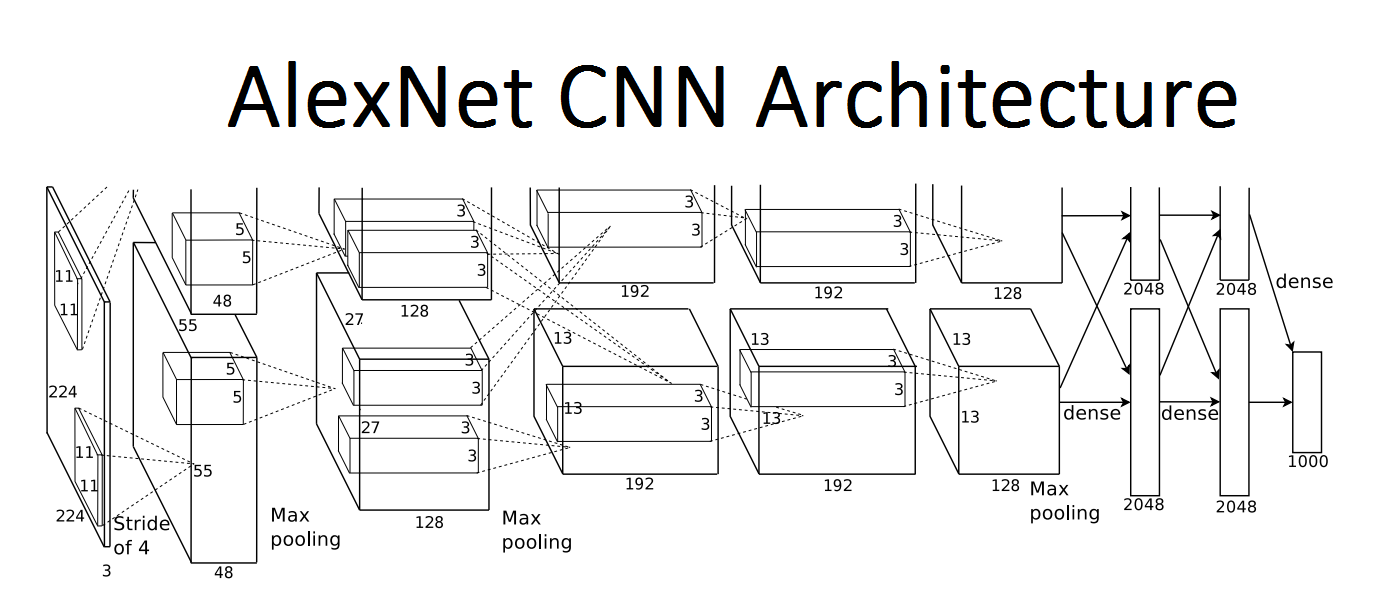
Note: The first real breakthrough in image classification was made by the AlexNet architecture.
Linear Model (Reminder)
$x_j: X \to \mathbb{R}$ — numerical features
$$a(x, w) = f(\left< w, x\right>) = f\left(\sum\limits_{j=1}^n w_j x_j + b \right)$$where $w_1, \dots, w_n \in \mathbb{R}$ — feature weights, $b$ — bias
$f(z)$ — activation function, for example, $\text{sign}(z),\ \frac{1}{1+e^{-z}},\ (z)_+$
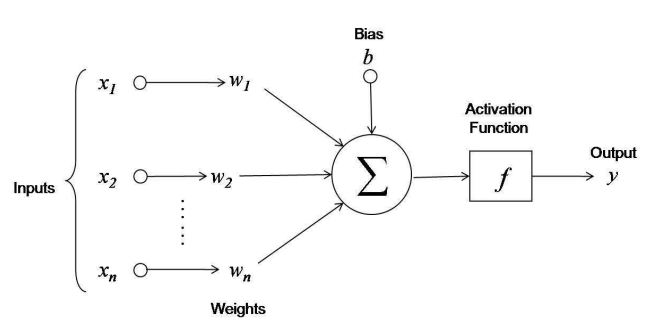
Neural network as a combination of linear models

Convolutional Neural Network
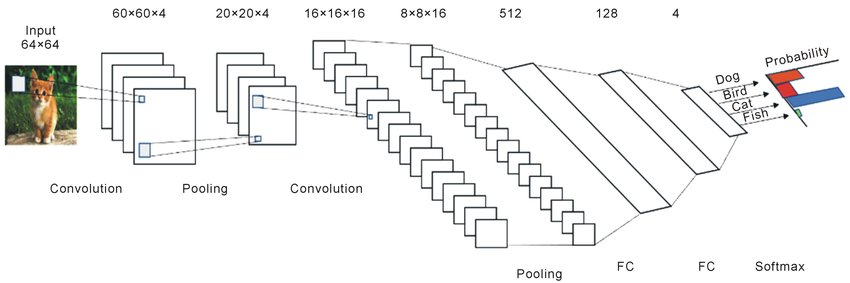
Convolution
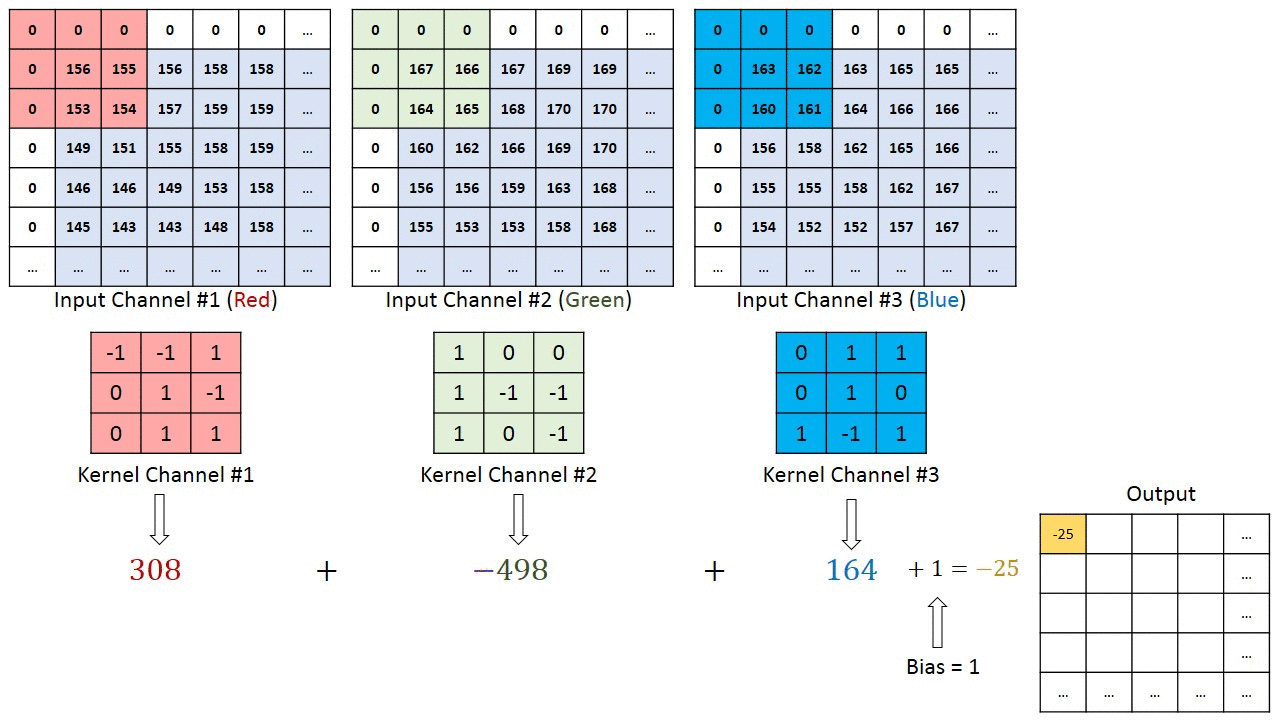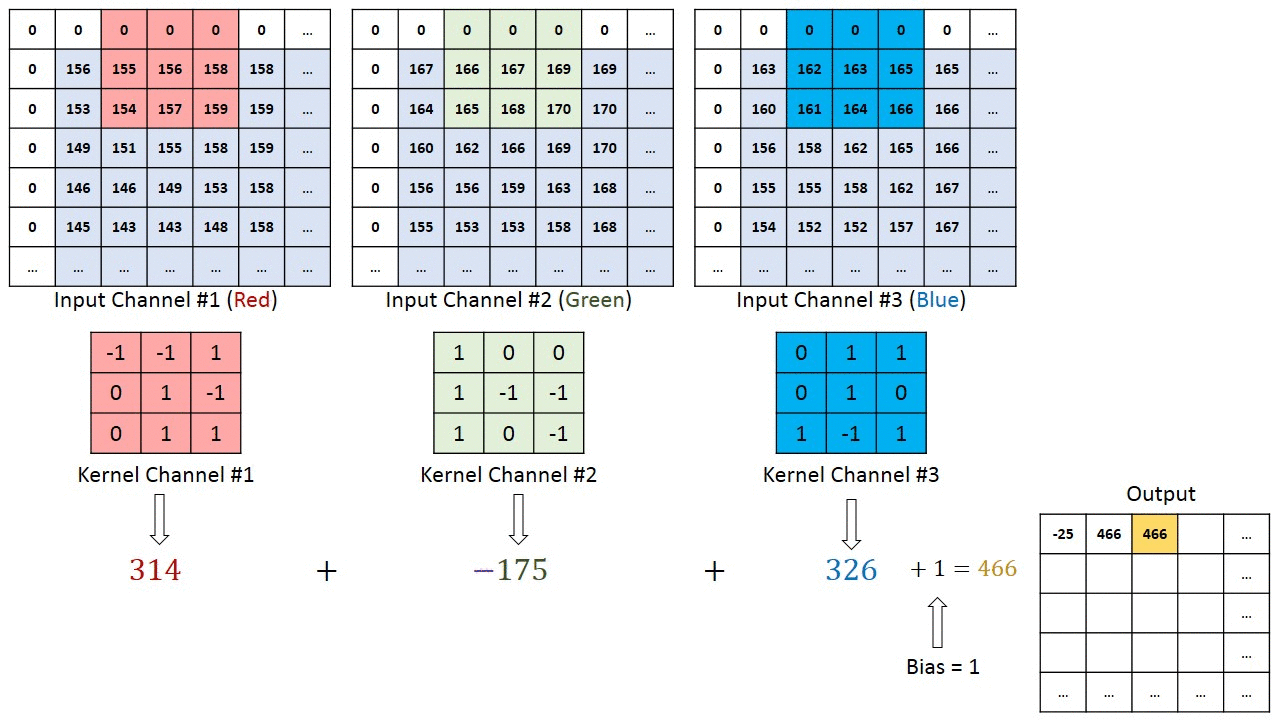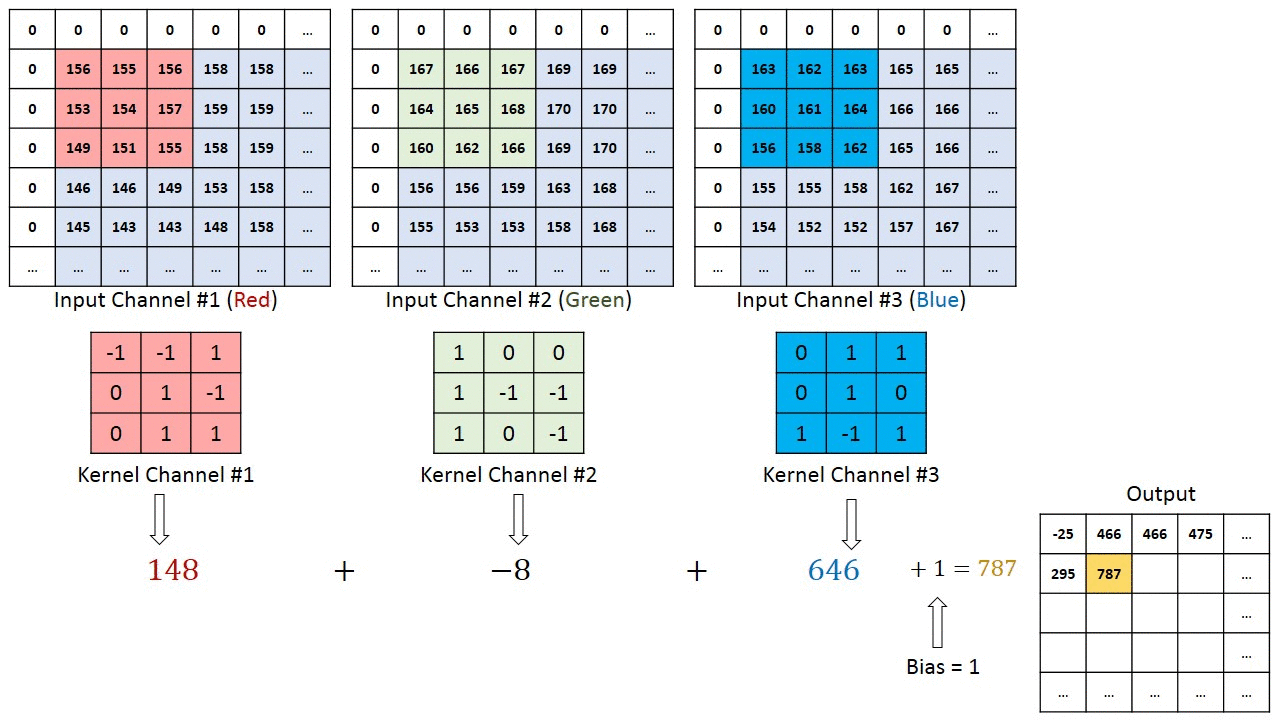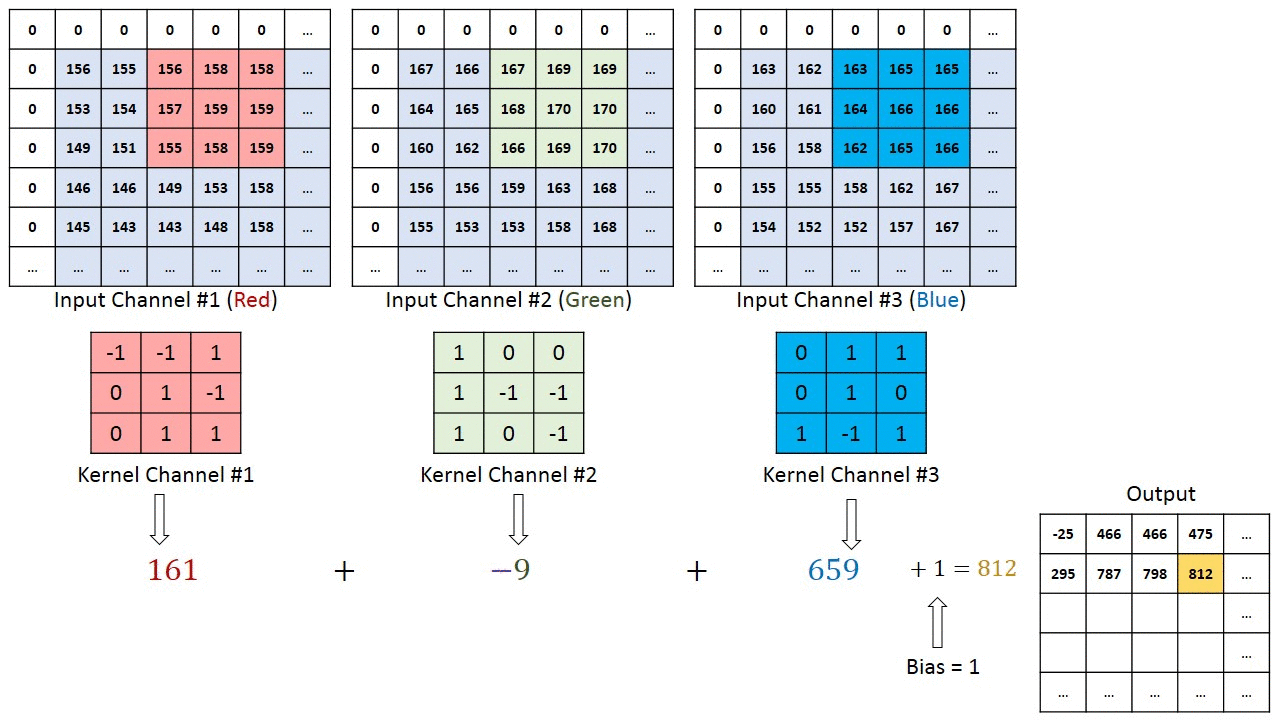
Convolution in neural networks — the sum of products of elements
- Radical reduction of training parameters $28^2 = 784 \to 9 = 3^2$ to get the same accuracy
- Directions $x$ and $y$ are built into the model
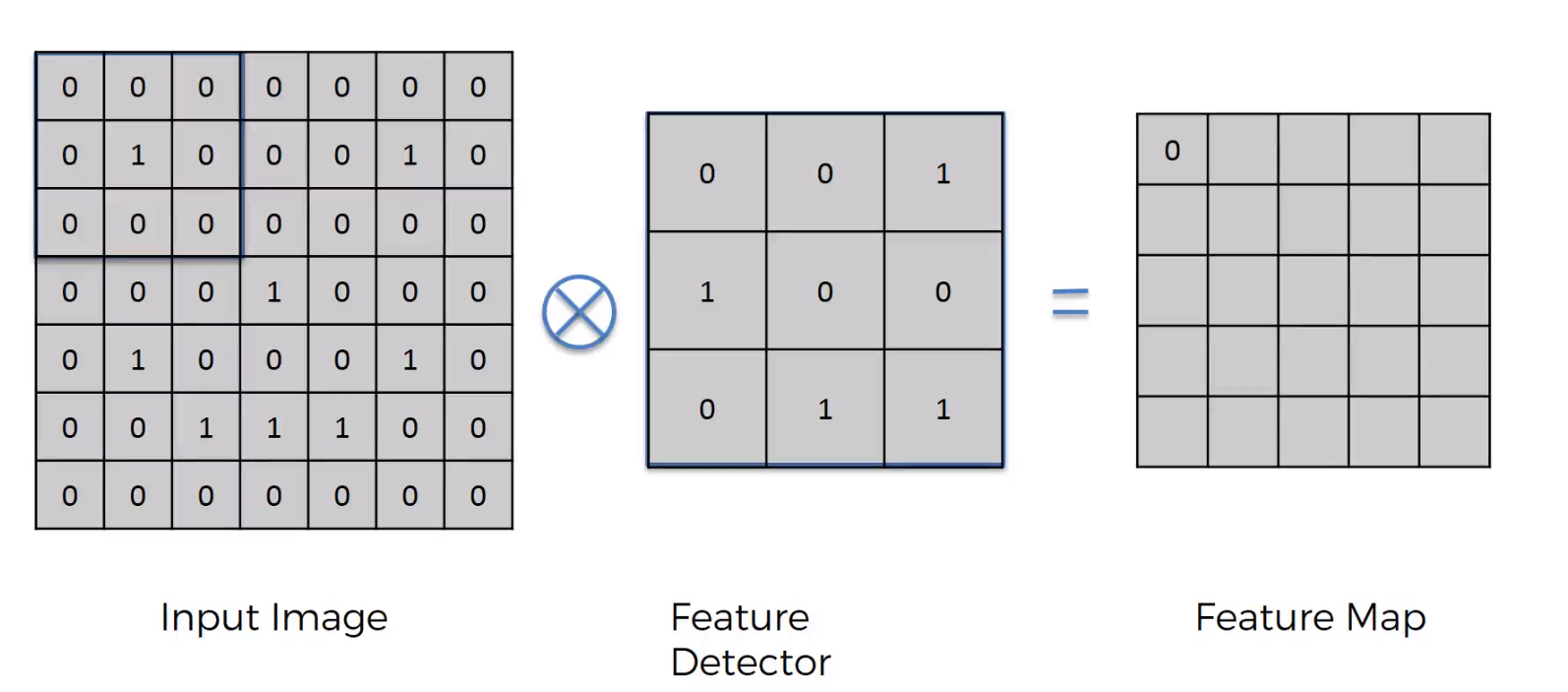
$\ \ $Question 1: Why is it called "convolution"?
Note
The implementation of convolution effectively multiplies a matrix by a vector. Here, for example, an article with the implementation of Winograd transformation in cuDNN
Convolution operation example
Kernel $3\times3\times3$ (Width $\times$ Height $\times$ Channel numbers)
Padding and stride
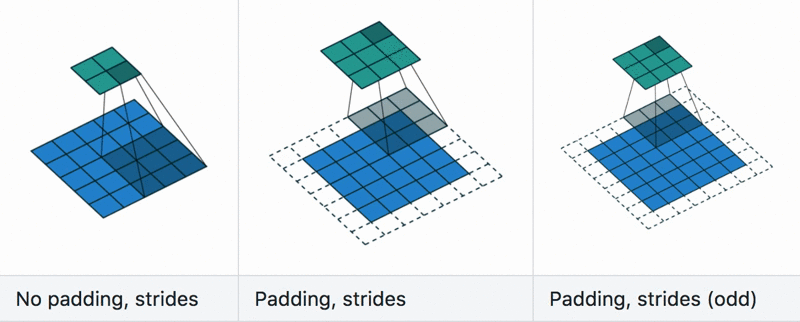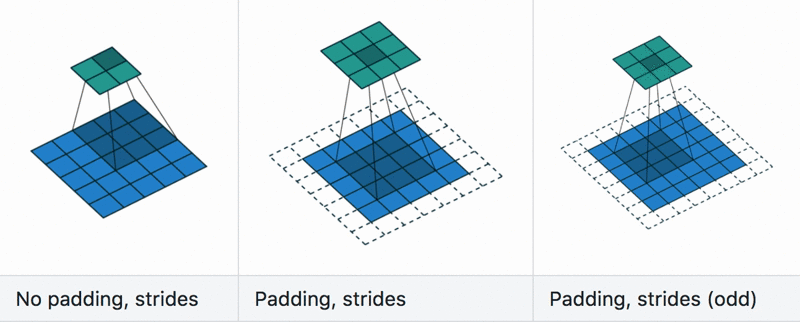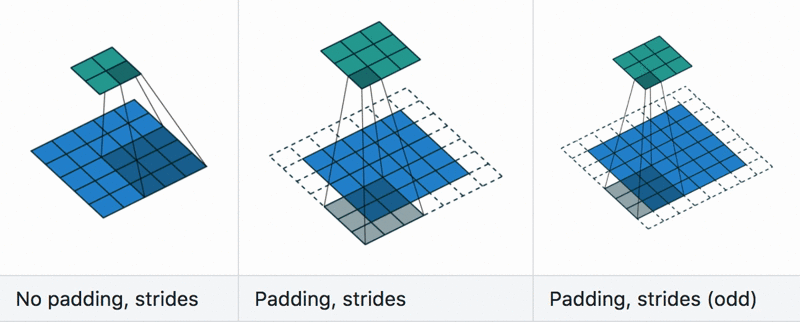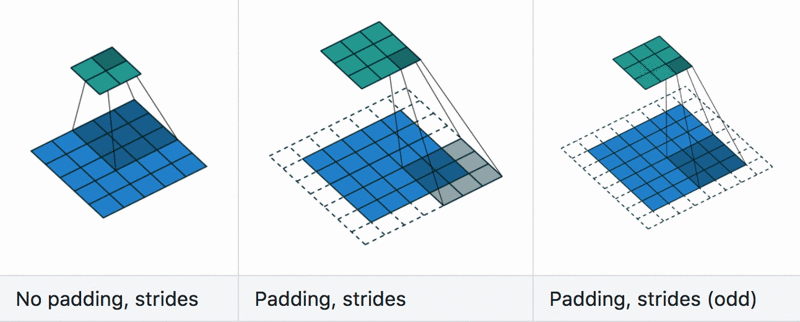
Dilation
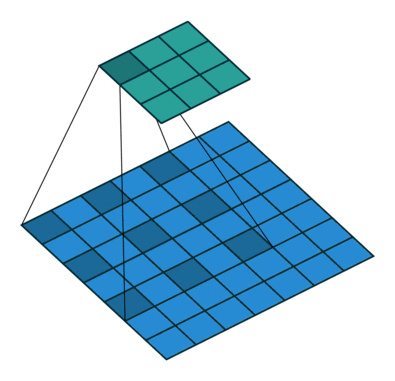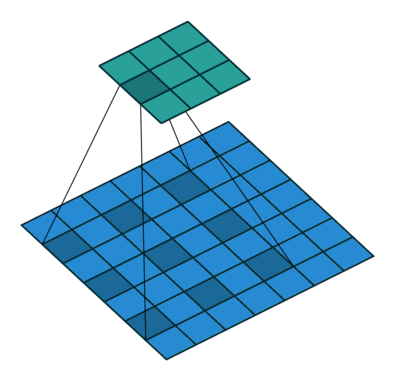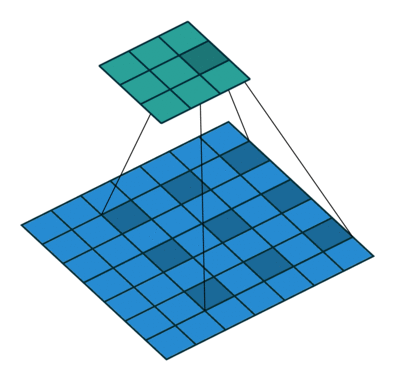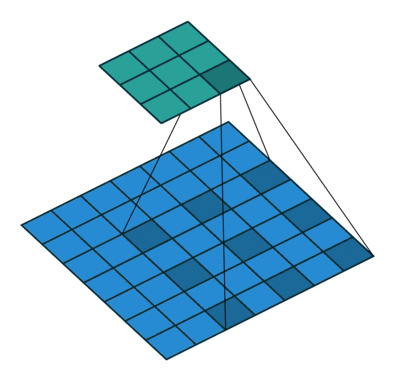
Calculate the size of the output
- Filter size = 3$\times$3 $\to$ 3
- Input size = 28$\times$28 $\to$ 28
- Stride = 1x1 $\to$ 1
- Padding = 0x0 $\to$ 0
Output size = (I - F + 2 * P) / S + 1 = (28 - 3 + 2*0) / 1 + 1 = 26
Output size = 26 $\to 26\times 26$
Pooling
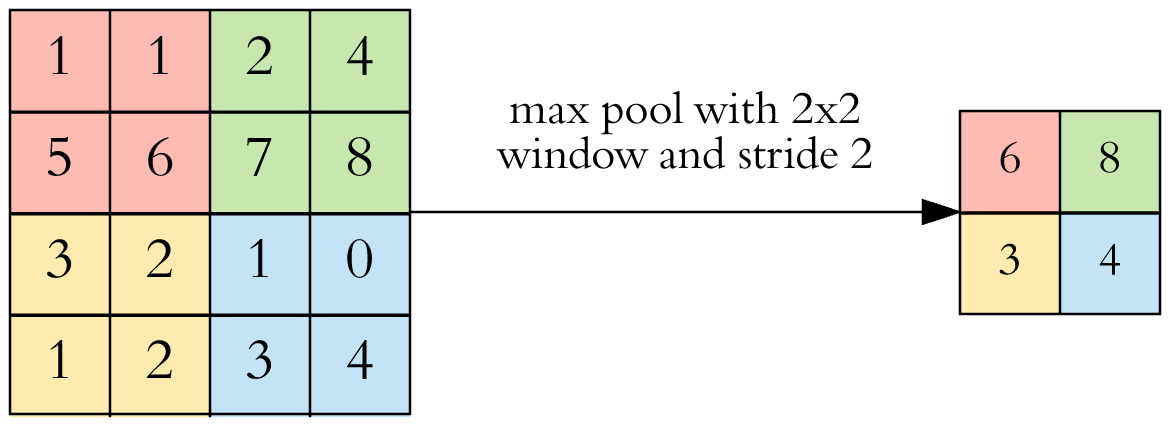
The pooling layer is maybe the simplest layer of all: we choose the maximum element from the filter. Or there is average pooling, where we take the average, but it is used quite rarely.
Activation Functions (Reminder)
- Logistic sigmoid: $\sigma(z) = \frac{1}{1+\exp(-z)}$
- Hyperbolic tangent: $\tanh(z) = \frac{\exp(z)-\exp(-z)}{\exp(z)+\exp(-z)}$
- Continuous approximations of threshold function
- Can lead to vanishing gradient problem and "paralysis" of the network
The progress of convolutional networks
Or a brief history of ImageNet
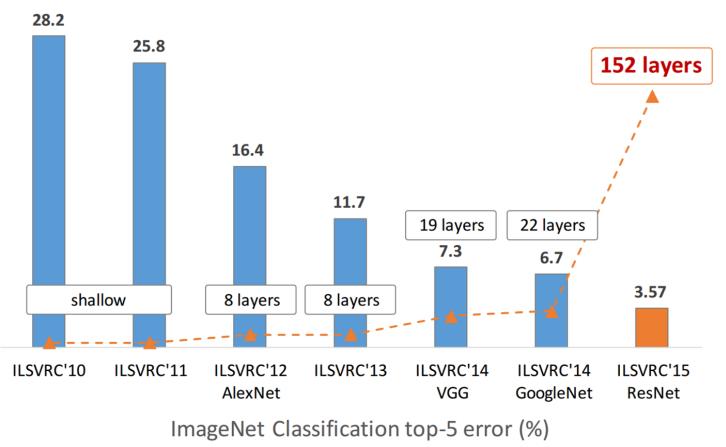
AlexNet (Krizhevsky, Sutskever, Hinton)
The Winner of the ImageNet contest of the 2012 year

Top5 final accuracy on ImageNet: 25.8% $\to$16.4%
- ReLU activation
- L2 regularization 5e-4
- Data augmentation
- Dropout 0.5
- Batch normalization (batch size 128)
- SGD Momentum 0.9
- Learning rate 1e-2, then decrease by 10 times after quality stabilization on the test
Momentum method
Momentum accumulation method [B.T.Polyak, 1964] — exponential moving average of the gradient over $\frac{1}{1-\gamma}$ last iterations:
$$\nu = {\color{orange}\gamma} \nu + {\color{orange}(1-\gamma)} \mathcal{L}_i^\prime(w)$$$w = w - \eta \nu$
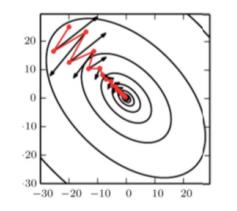
Note: from a physical point of view, the derivative of the loss function becomes the acceleration of the change in model parameters, and not the speed as in classical SGD
Summary
- Convolutional networks are very well-suited for image processing
- They are somewhat analogous to biological vision mechanisms
- At the same time, flexible and computationally efficient
- Today, they are the "de facto" standard for computer vision tasks like classification, detection, segmentation, and also are used in generation
What else can you watch?
- Demo by Andrej Karpathy
- There is a famous course from Stanford "CS231n: Convolutional Neural Networks for Visual Recognition": http://cs231n.github.io/
- About mechanistic interpretability, Anthropic employer Chris Olah by Lex Fridman, November 2024