Attention mechanism and Transformer architecture

Fundamentals of Machine Learning

Attention mechanism and Transformer architecture

Alex Avdiushenko
December 3, 2024

Disadvantages of vanilla Recurrent Neural Network (reminder)

We use one hidden vector

$$ h_t = f_W(h_{t-1}, x_t) $$

As a function $f_W$ we set a linear transformation with a non-linear component-wise "sigmoid":

$$ \begin{align*} h_t &= \tanh ({\color{orange}W_{hh}} h_{t-1} + {\color{orange}W_{xh}} x_t) \\ y_t &= {\color{orange}W_{hy}} h_t \end{align*} $$

Input and output sequence lengths must match
"Reads" the input only from left to right, does not look ahead
Therefore, it is not suitable for machine translation, question answering tasks, and others

RNN for sequence synthesis (seq2seq, reminder)

$X = (x_1, \dots, x_n)$ — input sequence

$Y = (y_1, \dots, y_m)$ — output sequence

$\color{green}c \equiv h_n$ encodes all information about $X$ to synthesize $Y$

$$ \begin{align*} h_i &= f_{in}(x_i, h_{i-1}) \\ {\color{green}h_t^\prime} &{\color{green}= f_{out}(h_{t-1}^\prime,y_{t-1},c)} \\ y_t &= f_{y}(h_t^\prime, y_{t-1}) \end{align*} $$

$$ \begin{align*} h_i &= f_{in}(x_i, h_{i-1}) \\ {\color{orange}h_t^\prime} &= f_{out}(h_{t-1}^\prime, y_{t-1}, c) \\ y_t &= f_{y}(h_t^\prime, y_{t-1}) \end{align*} $$

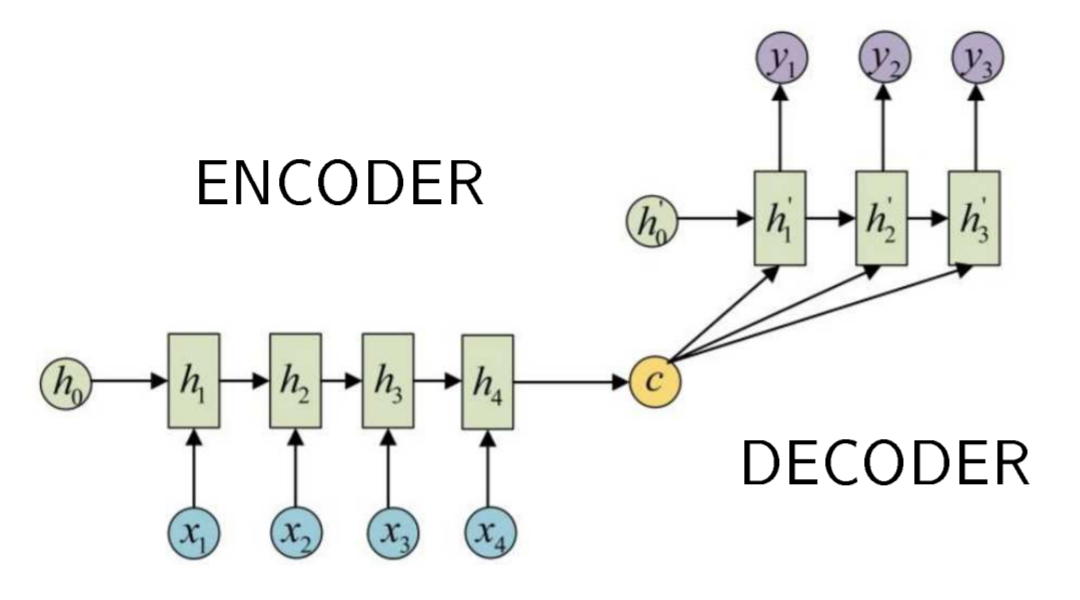
Disadvantages

${\color{green}c}$ remembers the end ($h_n$) better than the start
The more $n$, the more difficult to pack all the information into vector ${\color{green}c}$
We should control the vanishing and explosions of the gradient
RNN is difficult to parallelize

Question: How can you fix some of the problems above?

Hint: How do people perceive information?

Let's count the number of passes

Basketball!

RNN with an attention mechanism

$a(h, h^\prime)$ is the similarity function of input $h$ and output $h^\prime$ (for example, dot product or $\exp(h^T h^\prime)$ and others)

$\alpha_{ti}$ — importance of input $i$ for output $t$ (attention score), $\sum\limits_i \alpha_{ti} = 1$

$c_t$ — input context vector for output $t$

$$ \begin{align*} h_i &= f_{in}(x_i, h_{i-1}) \\ {\color{green}\alpha_{ti}} &= \text{norm}_i \, a(h_i, h^\prime_{t-1}), \, \text{ norm}_i(p) = \frac{p_i}{\sum\limits_j p_j} \\ {\color{green}c_t} &= \sum_i \alpha_{ti} h_i \\ h_t^\prime &= f_{out}(h^\prime_{t-1}, y_{t-1}, {\color{green}c_t}) \\ y_t &= f_{y}(h_t^\prime, y_{t-1}, {\color{green}c_t}) \end{align*} $$

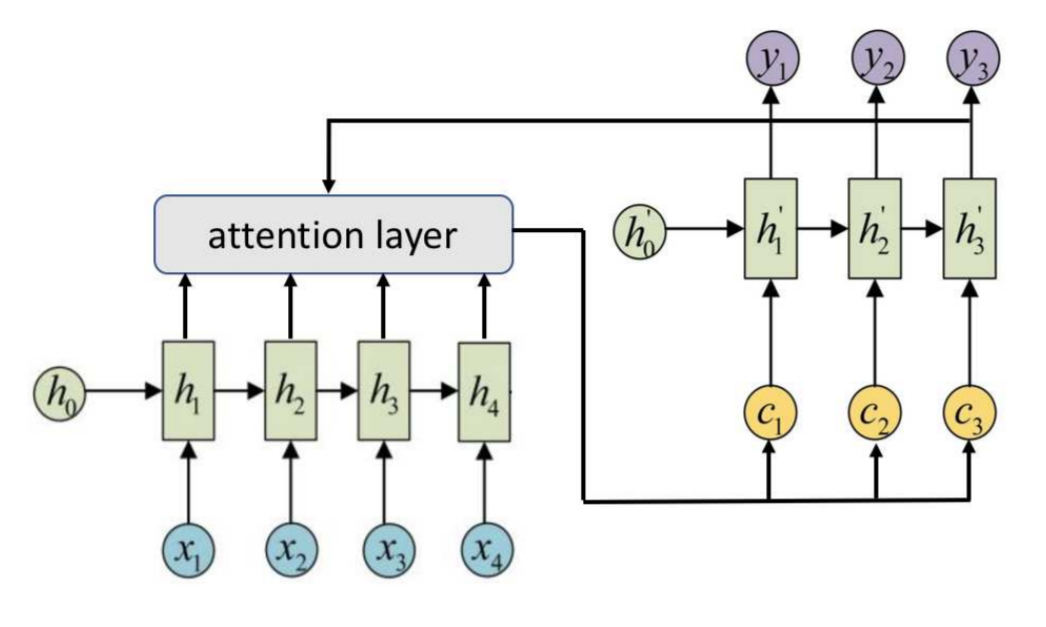
You can enter learnable parameters in ${\color{green}\alpha}$ and ${\color{green}c_t}$
It is possible to refuse recurrence both in $h_i$ and in $h_t^\prime$

Bahdanau et al. Neural machine translation by jointly learning to align and translate. 2015

The Main Areas for Attention Models

Converting one sequence to another, i.e., seq2seq:

Machine translation
Question answering
Text summarization
Annotation of images, videos (multimedia description)
Speech recognition
Speech synthesis

Sequence processing:

Classification of text documents
Document Sentiment Analysis

Attention in machine translation

English to French Translation with Attention

Attention Model Interpretability: Visualization of $\alpha_{ti}$

Attention for annotating images

When generating a word for an image description, the visualization shows which areas of the image the model pays attention to.

Kelvin Xu et al. Show, attend and tell: neural image caption generation with visual attention. 2016

Vector Similarity Functions

$a(h, h^\prime) = h^T h^\prime$ is the scalar (inner) product

$a(h, h^\prime) = \exp(h^T h^\prime)$ — with norm becomes SoftMax

$a(h, h^\prime) = h^T {\color{orange}W} h^\prime$ — with the learning parameter matrix $\color{orange}{W}$

$a(h, h^\prime) = {\color{orange}w^T} \tanh ({\color{orange}U}h + {\color{orange}V} h^\prime)$ is additive attention with ${\color{orange}w, U, V}$

Linear vector transformations: query, key, value:

$a(h_i, h^\prime_{t-1}) = ({\color{orange}W_k}h_i)^T ({\color{orange}W_q}h^\prime_{t-1}) / \sqrt{d}$

$\alpha_{ti} = \text{SoftMax}_i a(h_i, h^\prime_{t-1})$

$c_t = \sum\limits_i \alpha_{ti} {\color{orange}W_v} h_i$

${\color{orange}W_q}_{d \times dim(h^\prime)}, {\color{orange}W_k}_{d \times dim(h)}, {\color{orange}W_v} _{d \times dim(h)}$ — linear neuron weight matrices,

possible simplification: ${\color{orange}W_k} \equiv {\color{orange}W_v}$

Dichao Hu. An introductory survey on attention mechanisms in NLP problems. 2018

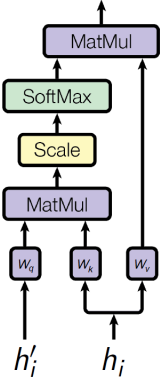
Attention Formula

$q$ is the query vector for which we want to calculate the context

$K = (k_1, \dots, k_n)$ — key vectors compared with the query

$V = (v_1, \dots, v_n)$ — value vectors forming the context

$a(k_i, q)$ — score of relevance (similarity) of a key $k_i$ to query $q$

$c$ is the desired context vector relevant to the query

Attention Model

This is a 3-layer network that computes a convex combination of $v_i$ values relevant to the query $q$:

\[ c = \text{Attn}(q,K,V) = \sum\limits_i v_i \, \text{SoftMax}_i \, a(k_i, q) \]

$c_t = \text{Attn}({\color{orange}W_q} h^\prime_{t-1}, {\color{orange}W_k} H, {\color{orange}W_v} H)$ is the example from the previous slide, where $H = (h_1, \dots, h_n)$ are input vectors, $h^\prime_{t-1}$ is output

Self-attention:

$c_i = \text{Attn}({\color{orange}W_q} h_{i}, {\color{orange}W_k} H, {\color{orange}W_v} H)$ is a special case when $h^\prime \in H$

Multi-Head Attention

Idea: $J$ different attention models are jointly trained to highlight various aspects of the input information (for example, parts of speech, syntax, idioms):

$ c^j = \text{Attn}({\color{orange}W^j_q} q, {\color{orange}W^j_k} H, {\color{orange}W^j_v} H), j = 1, \dots, J$

Variants of aggregating the output vector:

$ c = \frac{1}{J} \sum\limits_{j=1}^J c^j$ — averaging
$ c = [c^1 \dots c^J]$ — concatenation
$ c = [c^1 \dots c^J] {\color{orange}W}$ — to return to the desired dimension

Regularization: to make aspects of attention as different as possible, rows $J \times n$ of matrices $A, \alpha_{ji} = \text{SoftMax}_i a({\color{orange}W_k^j}h_i, {\color{orange}W_q^j}q)$, decorrelated $(\alpha_{s}^T\alpha_{j} \to 0)$ and sparse $(\alpha_{j}^T\alpha_{j} \to 1)$:

$\|AA^T - I \|^2 \to \min\limits_{\{{\color{orange}W_k^j}, {\color{orange}W_q^j}\}} $

Zhouhan Lin, Y.Bengio et al. A structured self-attentive sentence embedding. 2017

Transformer for Machine Translation

It is a neural network architecture based on attention and fully connected layers, without RNN. Scheme of transformations in machine translation:

$S = (w_1, \dots, w_n)$ — sentence from words in the input language

$\downarrow$ trainable or pre-trained word vectorization $\downarrow$

$X = (x_1, \dots, x_n)$ — embeddings of input sentence words

$\downarrow$ encoder transformer $\downarrow$

$Z = (z_1, \dots, z_n)$ — contextual embeddings

$\downarrow$ transformer-decoder $\downarrow$

$Y = (y_1, \dots, y_m)$ — embeddings of output sentence words

$\downarrow$ generation of words from the constructed language model $\downarrow$

$\tilde S = (\tilde w_1, \dots, \tilde w_m)$ — sentence words in target language

Vaswani et al. (Google) Attention is all you need. 2017

Architecture of Transformer: Encoder

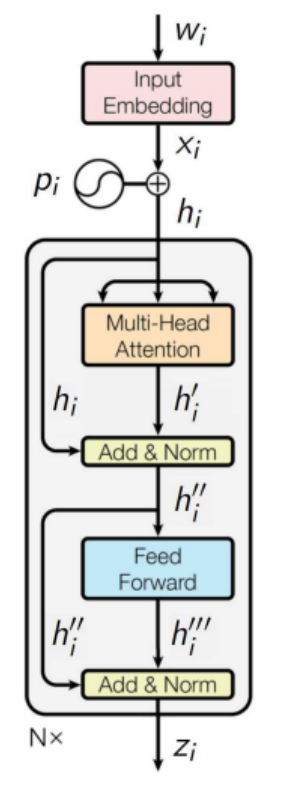
Position vectors $p_i$ are added:

$h_i = x_i + p_i, \ H = (h_1, \dots, h_n)$

$\scriptscriptstyle d = \text{dim } x_i, p_i, h_i = 512$
$\scriptscriptstyle \text{dim } H = 512 \times n$

Multi-head self-attention:

$h_i^j = \text{Attn}({\color{orange}W_q^j} h_{i}, {\color{orange} W_k^j} H, {\color{orange}W_v^j} H)$

$\scriptscriptstyle j = 1, \dots, J = 8$
$\scriptscriptstyle \text{dim } h_i^j = 64$
$\scriptscriptstyle \text{dim } W_q^j, W_k^j, W_v^j = 64 \times 512$

Concatenation:

$h_i^\prime = MH_j(h_i^j) \equiv [h_i^1 \dots h_i^J]$

$\scriptscriptstyle \text{dim } h_i^\prime = 512$

Skip-connection and layer normalization:

$h_i^{\prime\prime} = LN(h_i^\prime + h_i; {\color{orange}\mu_1, \sigma_1})$

$\scriptscriptstyle \text{dim } h_i^{\prime\prime}, \mu_1, \sigma_1 = 512$

Architecture of Transformer: Encoder

Fully connected two-layer network FFN:

$h_i^{\prime\prime\prime} = {\color{orange} W_2} \text{ReLU}({\color{orange} W_1}h_i^{\prime\prime} + {\color{orange} b_1}) + {\color{orange} b_2}$

$\scriptscriptstyle \text{dim } W_1 = 2048 \times 512$
$\scriptscriptstyle \text{dim } W_2 = 512 \times 2048$

Skip-connection and layer normalization:

$z_i = LN(h_i^{\prime\prime\prime} + h_i^{\prime\prime}; {\color{orange}\mu_2, \sigma_2})$

$\scriptscriptstyle \text{dim } z_i, \mu_2, \sigma_2 = 512$

Additions and Remarks

A lot of such blocks $N=6, h_i \to \square \to z_i$ are connected in series
Calculations can be easily parallelized in $x_i$
It is possible to use pre-trained $x_i$ embeddings
It is possible to learn embeddings $x_i$ of words $w_i \in V$
Layer Normalization (LN), $x, {\color{orange}\mu}, {\color{orange}\sigma} \in \mathbb{R}^d$

$$ LN_s(x; {\color{orange}\mu}, {\color{orange}\sigma}) = {\color{orange}\mu_s} + {\color{orange}\sigma_s} \frac{x_s - \overline{x}}{\sigma_x} $$ $$ \overline{x} = \frac{1}{d} \sum\limits_{s=1}^d x_s, \ \sigma_x^2 = \frac{1}{d} \sum\limits_{s=1}^d (x_s - \overline{x})^2 $$

Positional Encoding

The positions of the words $i$ are encoded by the vectors $p_i$ so that:

The more $|i-j|$, the more $\|p_i-p_j\|$
The number of positions is not limited

For example,

\[ h_j = \text{Attn}(q_j, K, V) = \sum_i (v_i + {\color{orange}w^v_{i\boxminus j}}) \text{SoftMax}_i a(k_i + {\color{orange} w^k_{i\boxminus j}}, q_j), \]

where $i\boxminus j = \max(\min(i-j, \delta), -\delta)$ is the truncated difference, $\delta = 5..16$

Shaw, Uszkoreit, Vaswani. Self-attention with relative position representations. 2018

Architecture of Transformer: Decoder

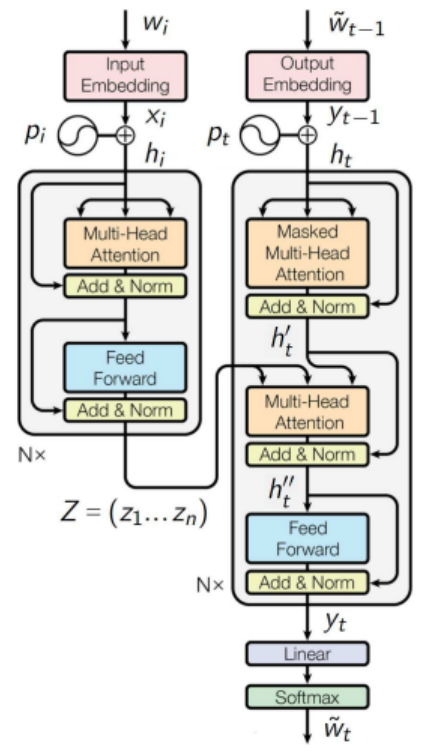
Autoregressive sequence synthesis

$y_0 = \left< \text{BOS} \right>$ — start symbol embedding;

For all $t = 1, 2, \dots$:

Masking data "from the future":
$h_t = y_{t-1} + p_t; \ H_t = (h_1, \dots, h_t)$

Multi-head self-attention:

$h_t^\prime = {\color{olive} LN_{sc}} \circ MH_j \circ \text{Attn}({\color{orange}W_q^j} h_{t}, {\color{orange} W_k^j} H_t, {\color{orange}W_v^j} H_t)$

Multi-head attention on the Z vectors:

$h_t^{\prime\prime} = {\color{olive} LN_{sc}} \circ MH_j \circ \text{Attn}({\color{orange}\tilde W_q^j} h_{t}^\prime, {\color{orange}\tilde W_k^j} Z, {\color{orange}\tilde W_v^j} Z)$

Architecture of Transformer Decoder

Two-layer neural network:

$y_t = {\color{olive} LN_{sc}} \circ \text{FFN}(h_t^{\prime\prime})$

Linear predictive layer:

$p(\tilde w|t) = \text{SoftMax}_{\tilde w}({\color{orange} W_y} y_t + {\color{orange} b_y})$

Generation $\tilde w_t = \arg\max\limits_{\tilde w} p(\tilde w|t)$
until $\tilde w_t \neq \left< \text{EOS} \right>$

Training and Validation Criteria for Machine Translation

Criteria for learning parameters of the neural network ${\color{orange}{W}}$ on the training set of sentences $S$ with translation $\tilde S$:

$$ \sum\limits_{(S, \tilde S)} \sum\limits_{\tilde w_t \in \tilde S} \ln p(\tilde w_t|t, S, {\color{orange}W}) \to \max\limits_W $$

Criteria for evaluating models (non-differentiable) based on a sample of pairs of sentences "translation $S$, standard $S_0$":

BiLingual Evaluation Understudy:

$\text{BLEU} = \min \left(1, \frac{\sum \text{len}(S)}{\sum \text{len}(S_0)} \right) \times $
$\underset{(S_0, S)}{\text{mean}}\left(\prod\limits_{n=1}^4 \frac{\#n\text{-gram from } S, \text{incoming in } S_0}{\#n\text{-gram in } S} \right)^{\frac14}$

BERT — Bidirectional Encoder Representations from Transformers

The BERT transformer is a decoderless encoder that can be trained to solve a wide range of NLP problems. Scheme of data transformations in NLP tasks:

$S = (w_1, \dots, w_n)$ — sentence from words in the input language

$\downarrow$ learning embeddings with transformer $\downarrow$

$X = (x_1, \dots, x_n)$ — embeddings of input sentence words

$\downarrow$ encoder transformer $\downarrow$

$Z = (z_1, \dots, z_n)$ — contextual embeddings

$\downarrow$ additional training for a specific task $\downarrow$

$Y$ — output text / markup / classification, etc.

Jacob Devlin, Ming-Wei Chang, Kenton Lee, Kristina Toutanova (Google AI Language)
BERT: pre-training of deep bidirectional transformers for language understanding. 2019.

MLM (Masked Language Modeling) Criterion for BERT Training

The masked language modeling criterion is built automatically from texts (self-supervised learning):

$$ \sum\limits_{S} \sum\limits_{ i \in M(S)} \ln p(w_i|i, S, {\color{orange}W}) \to \max\limits_W, $$

where $M(S)$ is a subset of masked tokens from $S$,

$$ p(w|i, S, {\color{orange}W}) = \underset{w \in V}{\text{SoftMax}}({\color{orange}W_z}z_i(S, {\color{orange}W_T}) + {\color{orange}b_z})$$

is a language model that predicts the $i$-th sentence token $S$, $z_i(S, {\color{orange}W_T})$ is the contextual embedding of the $i$-th sentence token $S$ at the output of the transformer with parameters ${\color{orange}W_T}$, ${\color{orange}W}$ — all transformer and language model parameters

NSP (Next Sentence Prediction) Criterion for BERT Training

The criterion for predicting the relationship between NSP sentences is built automatically from texts (self-supervised learning):

$$ \sum\limits_{(S, S^\prime)} \ln p\left(y_{SS^\prime}|S, S^\prime, {\color{orange}W}\right) \to \max\limits_W, $$

where $y_{SS^\prime} = $ $\left[S\right.$ followed by $\left.S^\prime\right]$ is the binary classification of a pair of sentences,

$$ p(y|S, S^\prime, {\color{orange}W}) = \underset{y \in \{0,1\}}{\text{SoftMax}}\left({\color {orange}W_y} \tanh({\color{orange}W_s}z_0(S, S^\prime, {\color{orange}W_T}) + {\color{orange}b_s}) + {\color{orange}b_y}\right)$$

— probabilistic classification model for pairs $(S, S^\prime)$, $z_0(S, S^\prime, {\color{orange}W_T})$ — contextual embedding of token $\left<\text{CLS}\right>$ for a sentence pair written as $\left<\text{CLS}\right> S \left<\text{SEP}\right> S^\prime \left<\text{SEP}\right>$

A Few More Notes About Transformers

Fine-tuning: model $f(Z(S, {\color{orange}W_T}), {\color{orange}W_f})$, sample $\{S\}$ and criterion $\mathcal{L}(S, f) \to \max$
Multitask learning: for additional training on a set of tasks $\{t\}$, models $f_t(Z(S, {\color{orange}W_T}), {\color{orange}W_f})$, samples $\{S\}_t$ and sum of criteria $ \sum_t \lambda_t \sum_S \mathcal{L}_t(S, f_t) \to \max $
GLUE, SuperGLUE, Russian SuperGLUE — sets of test problems for understanding natural language
Transformers are usually built not on words, but on tokens received by BPE (Byte-Pair Encoding) or SentencePiece

First transformer: $N = 6, d = 512, J = 8$, weights 65M

$\text{BERT}_{\text{BASE}}$, GPT-1: $N = 12, d = 768, J = 12$, weights 110M

$\text{BERT}_{\text{LARGE}}$, GPT-2: $N = 24, d = 1024, J = 16$, weights 340M-1000M

GPT-3: weights 175 billion

Gopher (DeepMind): 280 billion

Turing-Megatron (Microsoft + Nvidia): 530 billion

Summary

Attention models were first built into RNNs or CNNs, but they turned out to be self-sufficient
Based on them, the Transformer architecture was developed, various variants of which (BERT, GPT, XLNet, ELECTRA, etc.) are currently SotA in natural language processing tasks, and not only
Multi-head self-attention (MHSA) has been proven to be equivalent to a convolutional network [Cordonnier, 2020]

Vaswani et al. Attention is all you need. 2017.
Dichao Hu. An Introductory Survey on Attention Mechanisms in NLP Problems. 2018.
Xipeng Qiu et al. Pre-trained models for natural language processing: A survey. 2020.
Cordonnier et al. On the relationship between self-attention and convolutional layers. 2020.

What Else Can You Look at?

GPT-3 on Wikipedia: https://en.wikipedia.org/wiki/GPT-3
Intro to LLMs by Andrej Karpathy, November 2023