nup_logo

Advanced machine learning

Model compression and Mixture-of-Experts


Alex Avdiushenko
May 6, 2025

Lecture Plan

  1. Quantization and Q-LoRA
  2. Pruning
  3. Distillation
  4. Sparse Mixture of Experts

Motivation for model compression

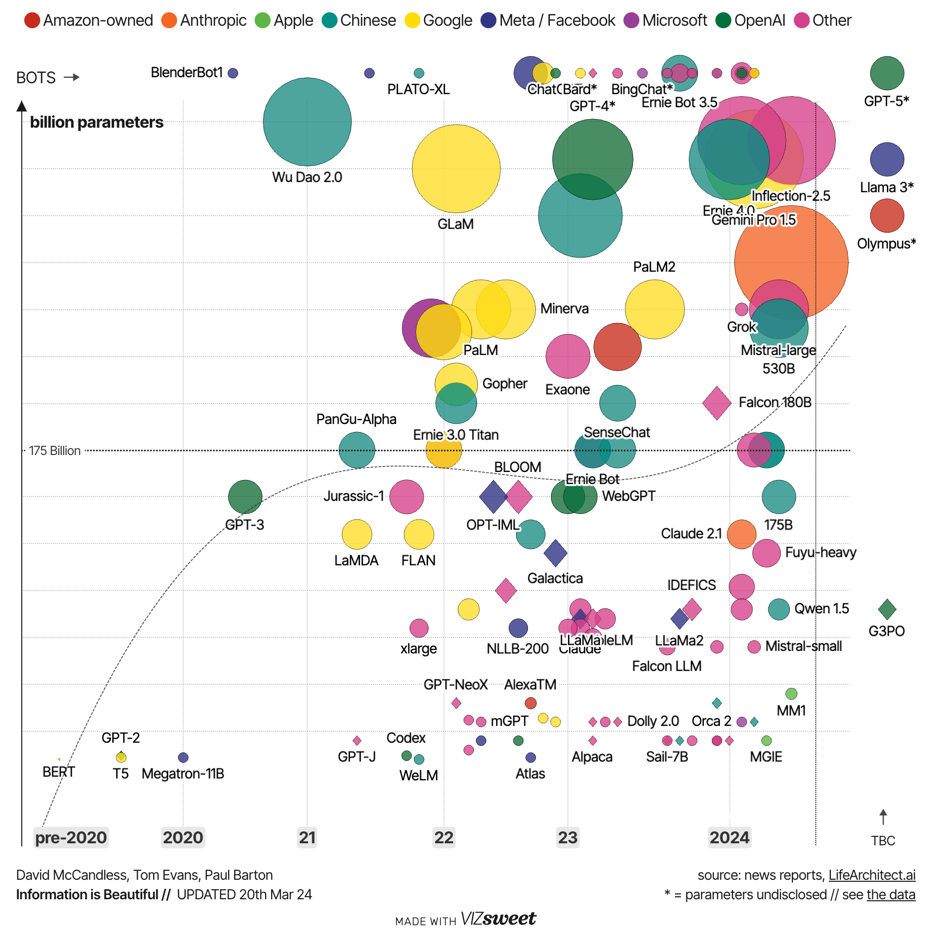
LLM_sizes

Motivation for model compression

  • LLM models are more and more massive
  • One week of ChatGPT usage ~= all the training cost
  • How can we cheaply, efficiently, and equitably deploy them without sacrificing performance?
  • Model compression
    • Quantization: keep the model the same but reduce the number of bits
    • Pruning: remove parts of a model while retaining performance
    • Distillation: train a smaller model to imitate the bigger model

Why is it possible to remove part of a big model?

In short: we don’t need all the parameters for the inference, but we need them for training.



We know for sure that half the stocks in our portfolio are worthless — the only problem is, we just don't know which half!

Post-Training Quantization


post-train-quantization

Int8 Quantization

  • Absolute Maximum (absmax) quantization:
$$ X_{i8} = \left\lfloor \frac{127 \cdot X_{f16}}{\max_{ij} (|X_{f16ij}|)} \right\rceil $$
  • This scales inputs to [-127, 127]

For 1d array [ 0.5, 20, -0.0001, -0.01, -0.1 ]

  • Maximum entry is 20
  • round(127/20 * [ 0.5, 20, -0.0001, -0.01, -0.1 ]) -> [ 3, 127, 0, 0, -1 ]

Layer-by-Layer Quantization-Aware Distillation

[Yao et al. 2022]

  • Initialize the quantized network with the same architecture as the original
  • Train each layer of the quantized network to mimic the output of its full-precision counterpart


Layer-by-Layer Quantization Illustration

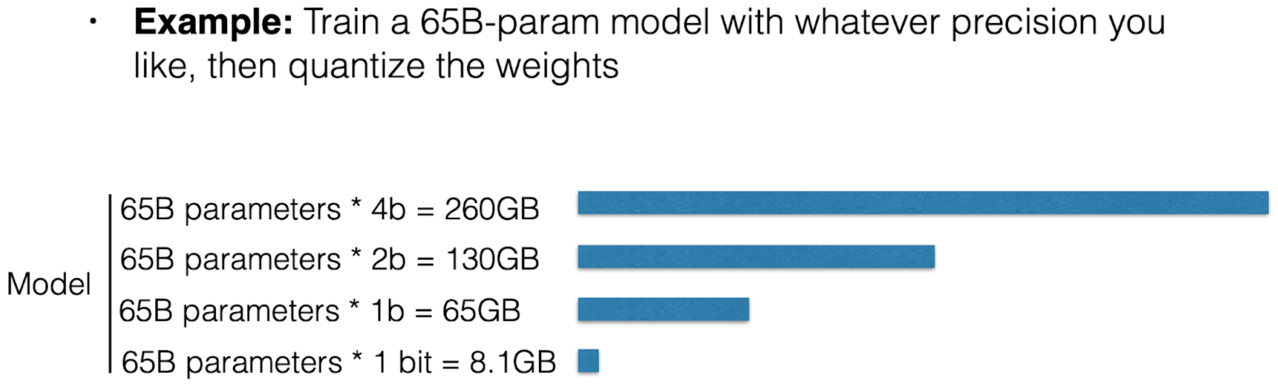
Q-LoRA

[Dettmers et al. 2023]

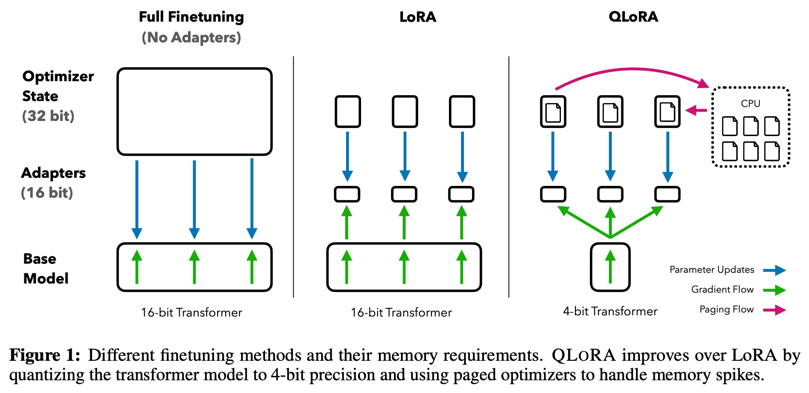
QLoRA Figure
  • Can train a 65B model on a 48GB GPU!

Pruning

Remove parameters from the model after training


Pruning vs Quantization

  • Quantization: no parameters are changed, up to $k$ bits of precision
  • Pruning: a number of parameters are set to zero, the rest are unchanged

Magnitude Pruning

[See et al. 2016], [Han et al. 2015]

  • Zero out the X% of parameters with the least magnitude
  • A type of unstructured pruning
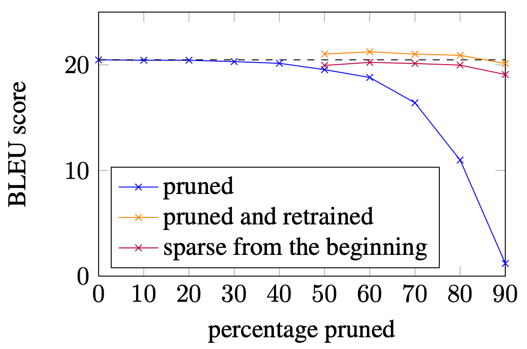
Magnitude Pruning BLEU Score Graph

Graph showing the BLEU score versus percentage of parameters pruned

Structured Pruning

[Xia et al. 2022]

  • Remove entire components
  • The remaining components aren’t pruned
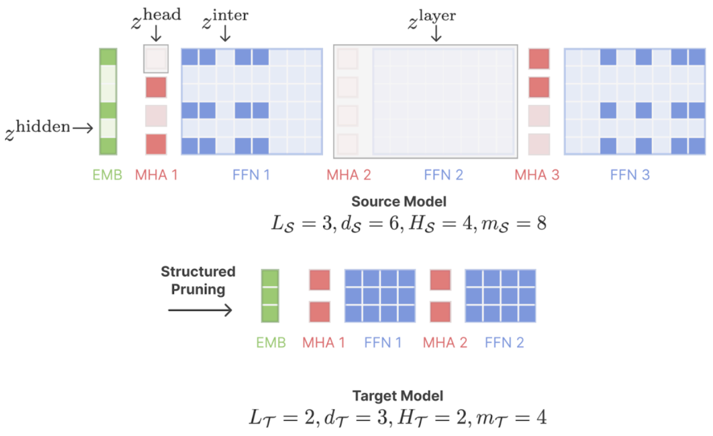
Structured Pruning Diagram

Pruning with only Forward Passes

[Dery et al. 2024]

  • Structured pruning of big models requires a lot of memory
  • Can we avoid using gradients?
  • Idea:
  1. Measure the performance of a model with different modules masked
  2. Learn the impact of each module mask via regression

Distillation

Train one model (the “student”) to replicate the behavior of another model (the “teacher”)


Distillation vs Quantization vs Pruning

  • Quantization: no parameters are changed, up to k bits of precision
  • Pruning: a number of parameters are set to zero, the rest are unchanged
  • Distillation: ~all parameters are changed

DistilBERT

[Sanh et al. 2019]

DistilBERT Performance Table

Performance comparison between models

A Toolkit for Synthetic Data Generation

[Patel et al. 2024]

  • "Hard target distillation"
Toolkit for Synthetic Data Generation Table

Mixture of Experts: Sparse Computation

  • What happens when a scalar-tensor multiplication is zero?

    • $0 \cdot [a, b, c] = [0, 0, 0]$

  • The result is guaranteed to be zero! No computation needed
  • This can happen in many parts of a model:
    • Single rows in a matrix multiply → optimized by GPU
    • Larger tensors → sparse MoE models
    • Whole models in an ensemble → just don’t use that model

Sparsely Gated Mixture of Experts Layer

[Shazeer et al. 2017]

  • Select a subset of FFNs to actually execute
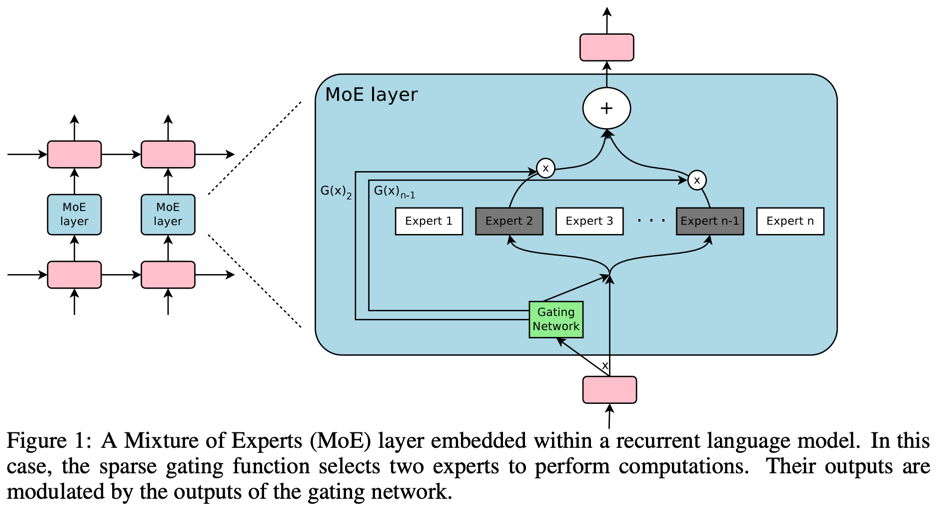
MoE Layer Diagram

$$ G(x) = \text{softmax}(\text{keep\_top\_k}(f_\text{gating}(x), k)) $$

$$ \text{keep\_top\_k}(v, k)_i = \begin{cases} v_i & \text{if } v_i \text{ is in the top k elements of } v \\ -\infty & \text{otherwise} \end{cases} $$

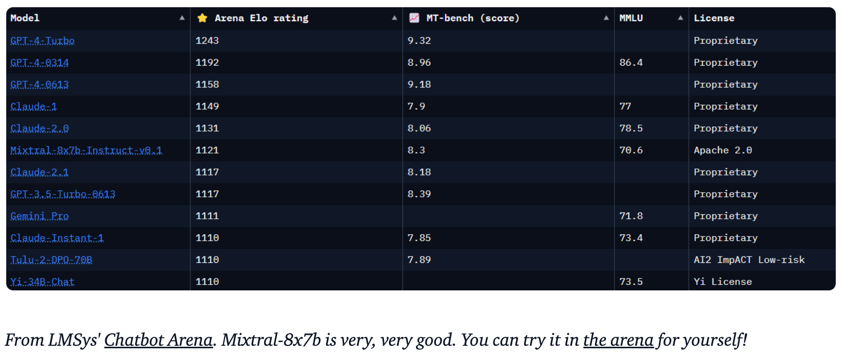
Mixtral_res.png

Understanding Mixtral-8x7b

The SMoE (Sparse-Mixture-of-Experts) MLP is Mixtral's distinct feature. It is the reason for its exceptional performance at low compute cost.

  • SMoEs trade high parameter count for computational efficiency by using multiple layers (experts) but only executing a few per input
  • The gating mechanism uses a learned linear layer to score each expert, and the top $k$ experts are selected for computation
  • The weighted summation only needs to occur over the chosen top experts, saving computation
https://huggingface.co/blog/vtabbott/mixtral

Summary

  1. Quantization and Q-LoRA
    • Quantization reduces the precision of model parameters (e.g., Int8) to save memory and computational resources
    • Q-LoRA allows fine-tuning large models (e.g., 65B) on resource-constrained hardware by using 4-bit quantization
    • May introduce a small accuracy loss if precision is too low
  2. Pruning
    • Pruning removes less significant parameters, reducing model size and computation
    • Magnitude pruning zeros out the lowest magnitude parameters, while structured pruning removes entire components
    • Structured pruning requires careful tuning to avoid significant performance drops
  1. Distillation
    • Distillation trains a smaller model (student) to imitate a larger model (teacher), retaining most of its performance
    • DistilBERT is an example, achieving comparable results to BERT with fewer parameters
    • Involves some performance trade-offs depending on task complexity
  2. Sparse Mixture of Experts (MoE)
    • Sparse MoE only activates a subset of experts (layers) for each input, drastically reducing computation
    • Mixtral-8x7b uses SMoE for efficient computation with high performance
    • Requires a gating mechanism to determine which experts to use for each input
  3. What else to look at? Scientific knowledge distillation from deep learning models