From AlphaGo to AlphaZero

Advanced machine learning

From AlphaGo to AlphaZero

Alex Avdiushenko
February 25, 2025

RL recap

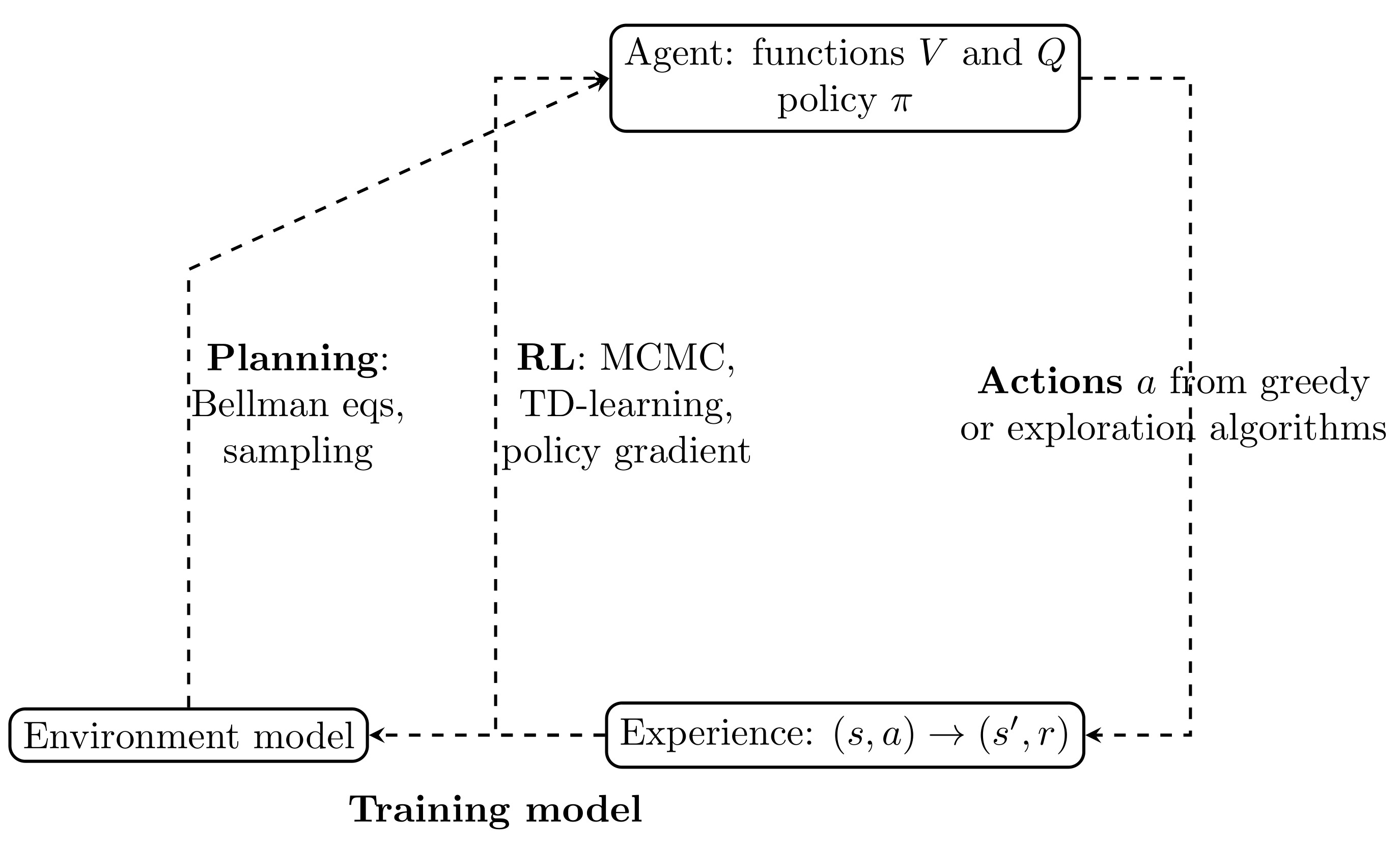
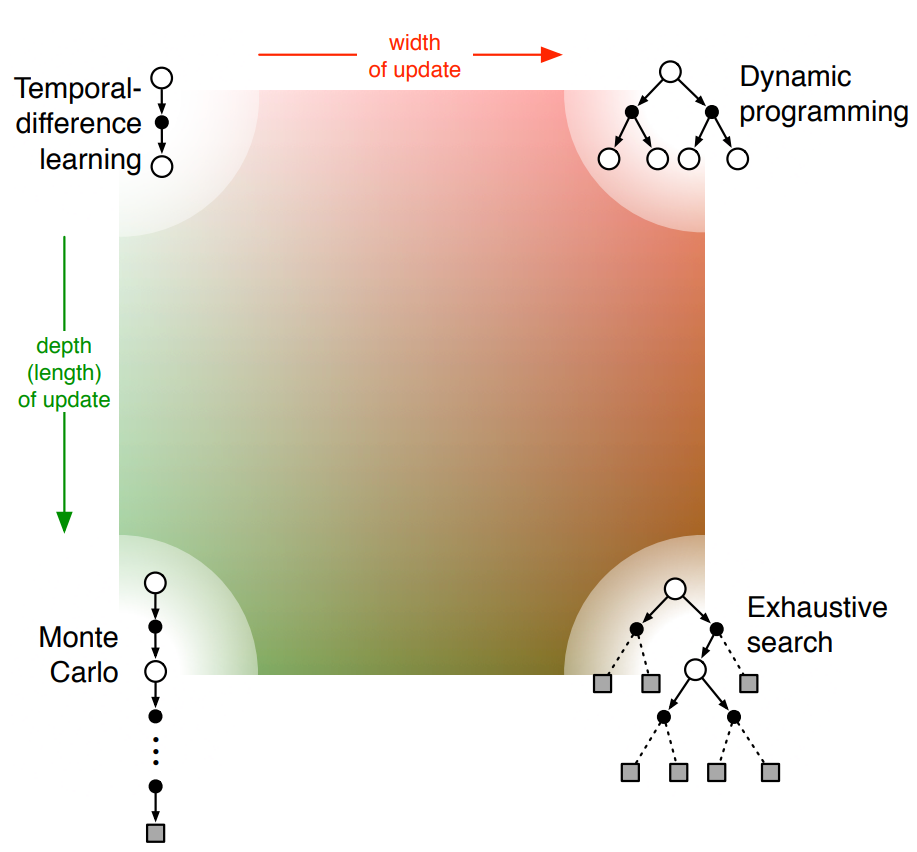
Source: BartoSutton.pdf

Policy gradient

We are trying to train just policy

$$\pi(a|s, \theta) = Pr[a_t = a| s_t = s]$$

We can train stochastic policies, where $\pi(a|s) \neq 0,1$
We even can train raw scores only, applying Softmax for moves probabilities

Policy gradient theorem

$$ \theta_{t+1} = \theta_{t} + \alpha \nabla_\theta J(\theta_t) \\ J(\theta) = V_{\pi_\theta}(s_0) \underset{\theta}{\to} \max \\[0.25cm] \boxed{\nabla_\theta J(\theta) \propto \sum\limits_s Pr_\pi[s] \sum\limits_a Q_\pi(s,a) \nabla_\theta \pi(a|s)} $$

Probabilities $Pr_\pi[s]$ are very hard to calculate, but we can just play using policy $\pi,$ and this gives us correct samples from this distribution

The REINFORCE algorithm is a policy-based method used in reinforcement learning. Unlike value-based methods, which aim to learn a value function by interaction with the environment, REINFORCE learns a stochastic policy directly.

$${\nabla_\theta J(\theta) \propto \sum\limits_s Pr_\pi[s] \sum\limits_a Q_\pi(s,a) \nabla_\theta \pi(a|s)} = \\ \quad = \mathbb{E}_{\pi} \left[ \sum\limits_a Q_\pi(S_t,a) \nabla_\theta \pi(a|S_t, \theta)\right]$$

So the SGD updates are

$$\theta_{t+1} = \theta_{t} + \alpha \sum\limits_a \hat Q_\pi(S_t,a,\theta) \nabla_\theta \pi(a|S_t, \theta),$$

where $\hat Q_\pi(S_t,a,\theta)$ is some learned approximation of the action-value function $Q$.

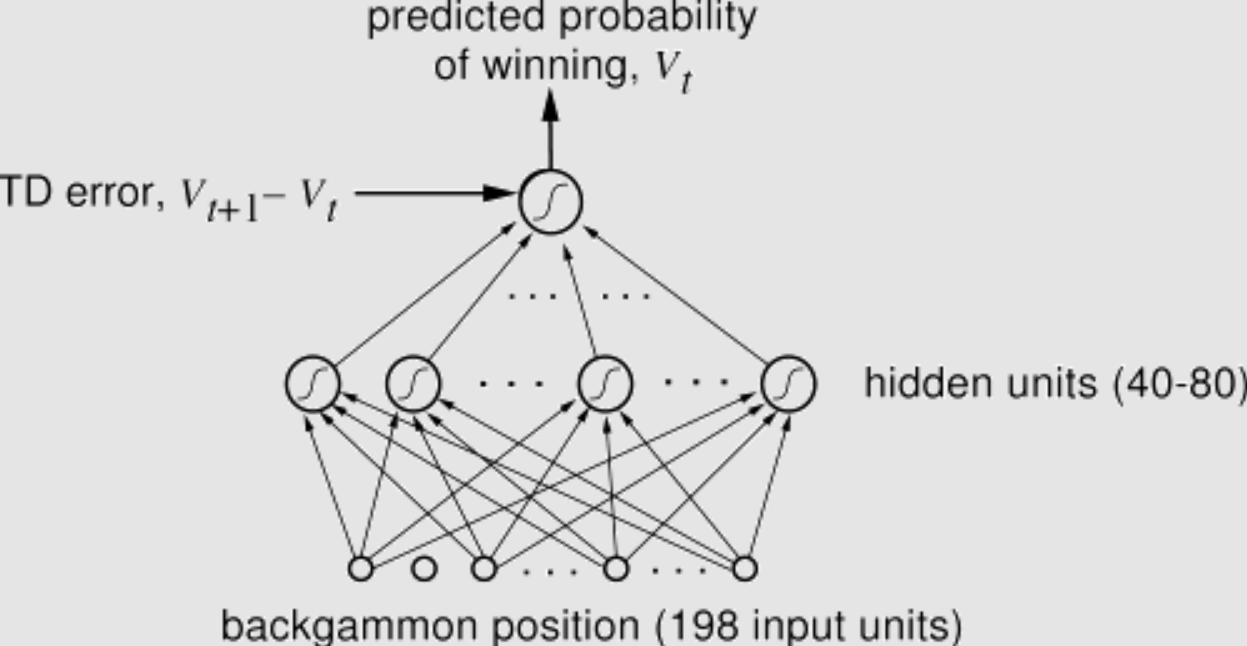
TD-Gammon (1992)

TD-Gammon is a computer gammon program that uses artificial intelligence and machine learning techniques to play the game at a highly competitive level. Developed by Gerald Tesauro from IBM.

TD-Gammon uses an algorithm called Temporal Difference (TD) learning. The core idea behind TD learning is that it learns directly from raw experience without any explicit supervisory signal. And firstly, people think that it works because of randomness internally embedded to gammon. TD-Gammon uses a multi-layer feed-forward neural network as its function approximator to generalize from its previous gameplay experience. The input to the network is the raw board position, and the output is a single number representing the program's prediction of the expected outcome. Despite being a program developed for a specific game, TD-Gammon's approach is widely applicable and has greatly influenced many other machine learning projects. It was one of the earliest successful demonstrations of a system that learns to improve its performance from raw experience using neural networks.

Game Go: Basic Rules

History of Programs Playing Go

1960-s: Beginnings

The first attempts to program a computer to play Go began in the 1960s
The earliest Go programs could only play on smaller 9x9 or 13x13 boards and demonstrated limited capabilities due to the complexity of the game and technological constraints. 1968: Albert Zobrist

1980-1990-s: Incremental Improvements

Throughout the 80s and 90s, Go programs gradually improved with advancements in computing power and AI algorithms
However, they were still far from matching the skills of human players. Goliath, Go Intellect, Handtalk, Goemate

The power of computer Go programs

1997: Janice Kim (1p) won HandTalk program with a 25-stone handicap
In the same year HandTalk program won 11-13 year old amateur 2-6 dans with 11-stone handicap
2001: Many Faces program won Insei (1p) on a 25-stone handicap
At the 2010 European Go Congress MogoTW played 19x19 Go against Catalin Taranu (5p). MogoTW received a 7-stone handicap and won
We know that DeepBlue defeated Garry Kasparov in 1997

What is the problem? Why is Go harder than Chess for computer?

Schematic tree of possible moves in Go

Why is Go really hard for computer?

Huge branching factor

Chess: there are 30–40 possibilities, and lots of them are obviously weak
Go: there are about 250 possibilities, and about 100 from them are "reasonable"

Hard to evaluate current position

Chess: one can count pieces material and there are simple heuristics
Go: it is really challenging even to understand who wins in the final position

2000-s: Monte-Carlo Tree Search

In the 2000s, Monte Carlo Tree Search (MCTS) algorithms were introduced, resulting in significant improvements in the performance of Go programs
We launch random simulations from the current position, observe which branches yield more wins, and then repeat the process

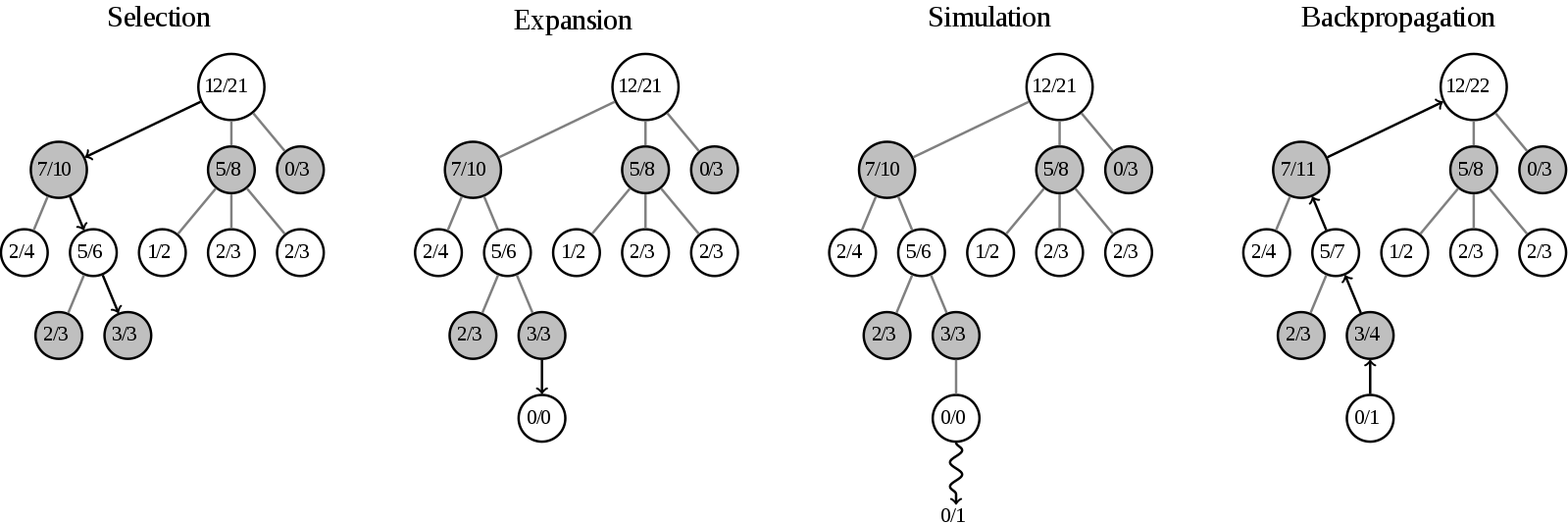
Monte Carlo Tree Search — UCB1

The main part of MCTS is the formula for selection of the next node. The UCB1 formula looks like this (the same as in multi-armed bandits):

$$ UCB1 = \frac{w_i}{n_i} + c \sqrt{\frac{\ln t}{n_i}} $$

where:

$w_i$ is the number of wins
$n_i$ is the count of simulations for the node associated with action $i$
$c$ is the parameter, by default $c=\sqrt{2}$
$t = \sum\limits_i n_i$ is the total count of simulations for the parent node

The algorithm prefers actions with higher estimated rewards and higher uncertainties.

AlphaGo vs. Lee Sedol
9-15 March 2016

Forecast was 1 : 4

Result was 4 : 1

And then, March 2016 became. This is a photo from a Go match in which the legendary Korean player Lee Sedol, one of the best in the world, is playing against an AI-based program, AlphaGo. Before the match, Lee Sedol, in fact being a very modest person, said that he would either win cleanly 5:0, or he might underestimate the strength of the program and somewhere due to a mistake, he would win 4:1. What do you think the result was? The computer won with a score of 4:1. It was so-called "sputnik"-moment for all Asia, when they truly understood that deep learning is huge thing.

History of AlphaGo

AlphaGo is a computer program developed by Google DeepMind in 2014-2015: David Silver, Aja Huang etc.
October 2015: AlphaGo plays its first match against the reigning three-time European Go champion, Fan Hui (2p), and wins 5:0. This is the first time a computer Go program has beaten a human professional player without handicaps on a full-sized 19x19 board.
Paper in Nature "Mastering the game of Go with deep neural networks and tree search"
March 2016: AlphaGo plays a five-game match against Lee Sedol, one of the world's top Go players, and wins 4:1
May 2017: AlphaGo plays a three-game match against Ke Jie, the world No.1 ranked player at the time, and wins 3:0

The development of AlphaGo was a significant achievement in the field of Artificial Intelligence.

What is inside AlphaGo?

Supervised learning (SL) policy network for next move prediction:
- 13-layers CNN for features extraction from the board
- 30 billion positions from human expert games
- Moves probability distribution as output: $p_\sigma(a \mid s)$
- Accuracy reaches 57%, which is very high
- Also train fast and worse strategy $p_\pi$ (accuracy is 24%, but inference time is much less: 3 millisecond $\to$ 2 nanosecond)

SL policy network predicts the next move

RL policy network improves SL using reinforcement learning:

the same structure of 13-layers CNN
initialize with SL policy network
self plays with one of the previous iterations of RL policy
new weights maximize the probability of winning
RL policy wins 80% games versus SL and 85% versus Pachi (one of the best MCTS programs)
and this is without any MCTS-counting, due to only the strong moves' prediction!

SL policy network predicts the next move
RL policy network improves SL using reinforcement learning

Also, they train function $V_\theta(s)$ for state evaluation:

the same structure of 13-layers CNN, but now output is the probability of winning
cannot train on the human expert's games only because of overfitting
so they used self-play games from the RL policy network
as a result, they got a great tool for position evaluation, which is 15K times faster than MCTS + RL

SL policy network predicts the next move
RL policy network improves SL using reinforcement learning
Function $V_\theta(s)$ for state evaluation

Eventually we can use MCTS counting:

build an MCTS-like tree
apriori probabilities initialize as $p_\sigma(a \mid s)$ from SL policy
in each node of a tree for state evaluation we use $V_\theta(s)$, combined with the random rollout of self-played fast strategy $p_\pi$
it is interesting that SL policy works better for tree building, but for training function $V_\theta(s)$ is better use stronger RL policy

AlphaZero

AlphaZero is a more generalized and simple variant of the AlphaGo algorithm, and is capable of playing Chess, Shogi and Go.

AlphaZero is a reinforcement learning system, it learns to play by playing games against itself and improving from its mistakes only
Silver et al., 2017: "Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm"
AlphaZero also outperformed Stockfish, one of the top-ranked chess engines, winning 28 games and drawing the rest in a 100-game match

Inside AlphaZero

we have only one deep neural network for next move prediction and position evaluation
it self-plays and simultaneously builds an MCTS tree
it improves both the NN weights (via RL) and MCTS tree

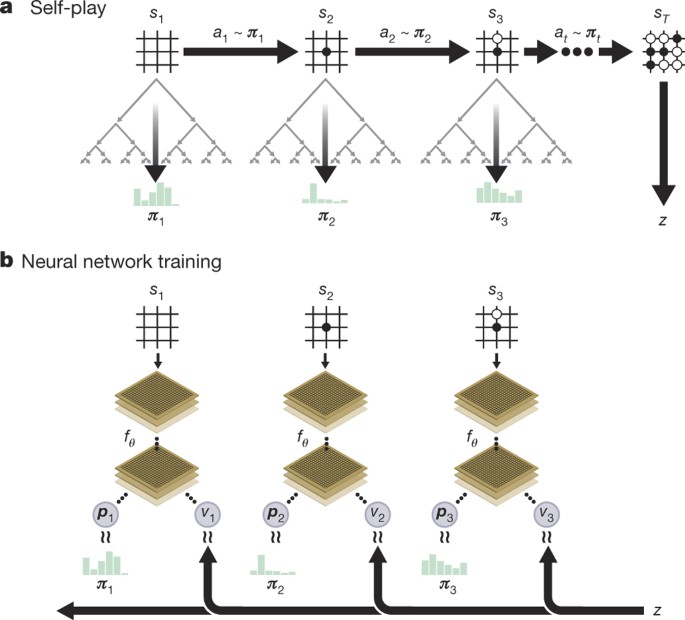
We minimize

$$ Loss = (z-v)^2 - \pi^T \cdot \log p + c \|\theta\|^2 $$

where $p$ is a vector with moves probabilities from NN, $\pi$ — improved by MCTS vector of probabilities, $z \in \mathbb{R}$ and $v \in \mathbb{R}$ are value function estimations from MCTS and NN, $\theta$ are weights of NN, and $c$ is regularization coefficient

Summary

We started with policy gradient descent (the central method in robotics)
We got acquainted with the AlphaGo and AlphaZero models
Reinforcement learning allows you to pass a gradient through a sequence of discrete steps with a reward at the end
Best used in tasks where there is a discrete sequence of actions and states

What else can you look at?

Educational resource on RL produced by OpenAI
Intro to RL with David Silver, DeepMind × UCL, 2015
Lecture by S. Nikolenko at Computer Science Club (in Russian)

Advanced machine learning