NLP crash intro

Advanced machine learning

NLP crash intro

Alex Avdiushenko
March 18, 2025

How to represent the meaning of a word?

It is a thesaurus developed since 2005

Problems with WordNet

New meaning of words, impossible to keep up-do-data
Subjective
Manually curated
Impossible to accurately compute word similarity

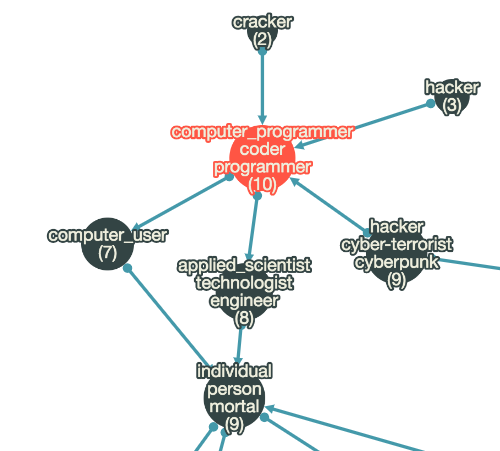
Distributional Hypothesis

A word’s meaning is given by the words that frequently appear close-by.

“You shall know a word by the company it keeps” (J. R. Firth 1957)
One of the most successful ideas of modern statistical NLP!

When a word $w$ appears in a text, its context is the set of words that appear nearby (within a fixed-size window). We use the many contexts of $w$ to build up a representation of $w$.

Example: Among all pets, **???** are the best at catching mice.

Word2Vec

Motivation

One-hot encoding representations:

Do not reflect the semantic similarity of words
Have too high dimensionality

One-hot simplified example:

Gym $\to [0, 1, 0, 0, 0, 0]$
Sofa $\to [0, 0, 1, 0, 0, 0]$
Rest $\to [0, 0, 0, 1, 0, 0]$

Continuous Bag of Words (CBOW) and Skip-gram

\[ \frac{1}{T}\sum\limits_{t=1}^T \log(p(w_{t}|w_{t-m}, \dots, w_{t-1}, w_{t+1}, \dots, , w_{t+m})) \]

\[ \frac{1}{T}\sum\limits_{t=1}^T \sum\limits_{-m \leq j \leq m, j \neq 0} \log(p(w_{t-j}|w_{t})) \]

Mikolov, Corrado, Chen, Dean "Efficient Estimation of Word Representations in Vector Space", 2013

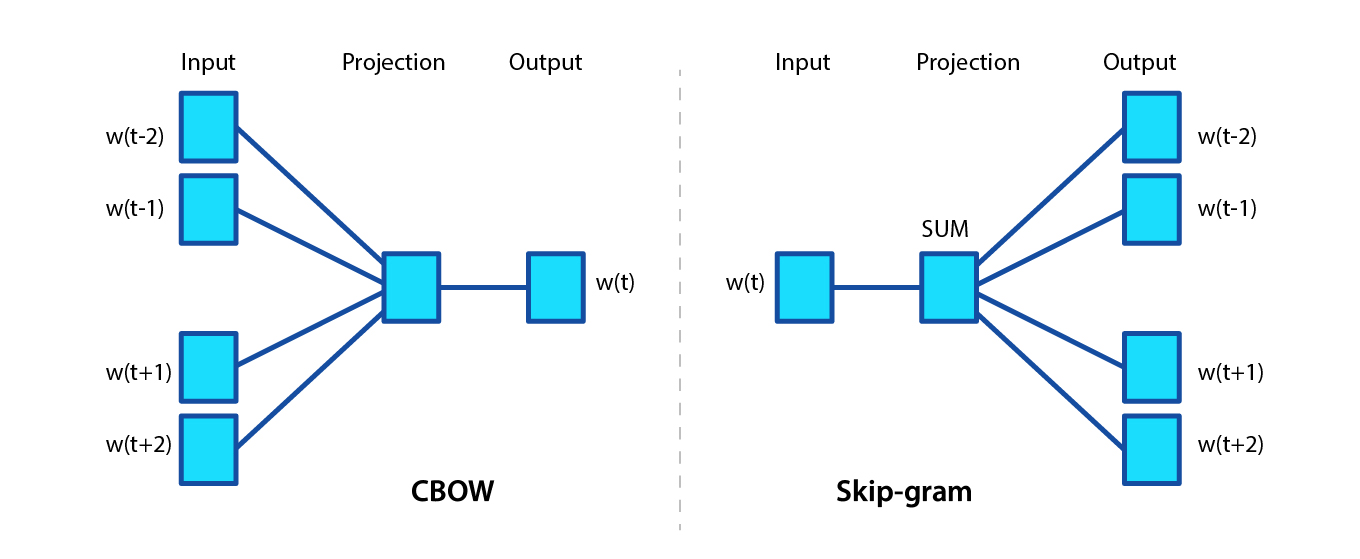
CBOW Model

The probability of word $w_t$ in a given context:

\[C_t = (w_{t-m}, \dots, w_{t-1}, w_{t+1}, \dots, w_{t+m})\] \[p(w_{t} = w|C_t) = \underset{w \in W}{\text{Softmax}} \left< u_w, v^{-t} \right>\]

$v^{-t} = \frac{1}{2m} \sum\limits_{w \in C_t} v_w$ — the average vector of words from the context $C_t$

$v_w$ — vectors of predicting words,

$u_w$ — vector of the predicted word, generally $u_w \neq v_w$

Criterion of maximum log-likelihood, $U, V \in \mathbb{R}^{|W| \times d}$:

$\sum\limits_{t=1}^n \log p(w_t|C_t) \to \max\limits_{U, V}$

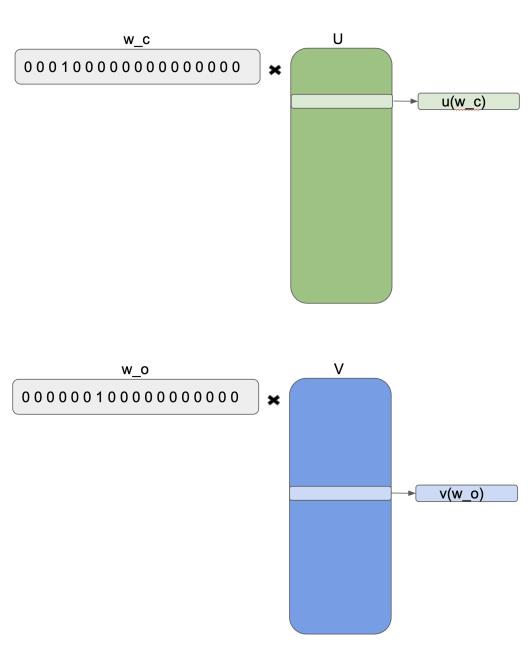
Skip-gram: How to Calculate Probabilities

$ p(w_o|w_c) = \frac{\exp[v(w_o)u^T(w_c)]}{\sum\limits_{w=1}^W \exp[v(w)u^T(w_c)]}$

$W$ — the set of all dictionary words

$w_c$ — central word

$w_o$ — context word

$u(\cdot)$ and $v(\cdot)$ — parameter vectors (embeddings), which are multiplied scalar-wise

What’s the problem with this approach?

In the denominator, of course, where all the words of the vocabulary are!

Mikolov proposed...

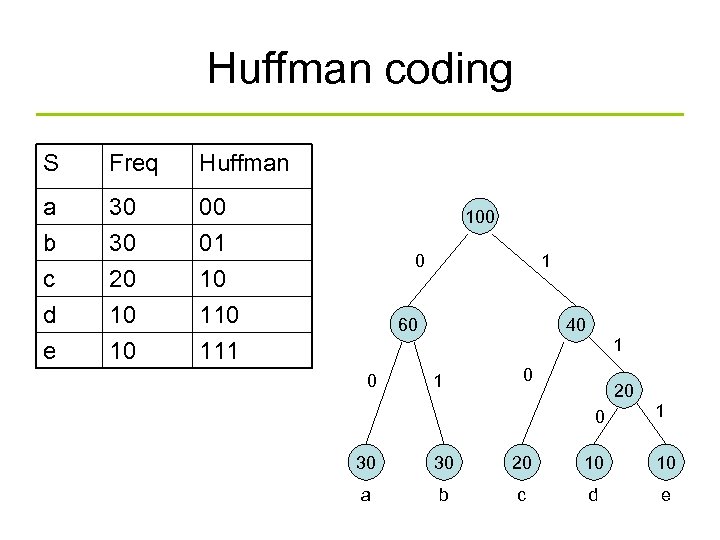
Hierarchical Softmax

We model the probability more efficiently by building a Huffman tree on the words, and then:

\[ 1 - \sigma(x) = \sigma(-x) \] \[ p(w_o|w_c) = \\ \prod\limits_{n \in \text{Path}(w_o)} \sigma(d_{nw_o} v(n) u^T(w_c))\]

Here, $v(n)$ is the trainable vector in the tree node, $d_{nw_o} = 1$ if $w_o$ is in the right subtree, $d_{nw_o} = -1$ otherwise.

doc2vec

\[u^\prime (\text{doc}) = \sum\limits_{w \in \text{doc}} \omega_w \cdot u(w)\]

As word weights $\omega_w$, it makes sense to use TF-IDF (term frequency / inverse document frequency)

GloVe (Global Vectors for Word Representation)

Motivation: Unlike Word2Vec, which is a predictive model, GloVe is a count-based model that leverages global statistical information about word occurrences.

The model captures word relationships using the following formula:

$X_{ij}$ — co-occurrence matrix where $X_{ij}$ is the frequency of word $j$ in the context of word $i$

\[ \log(X_{ij}) = w_i^T \tilde{w}_j + b_i + \tilde{b}_j \]

This equation models the ratio of co-occurrence probabilities to capture semantic relationships between words.

Pennington, Socher, Manning "GloVe: Global Vectors for Word Representation", 2014

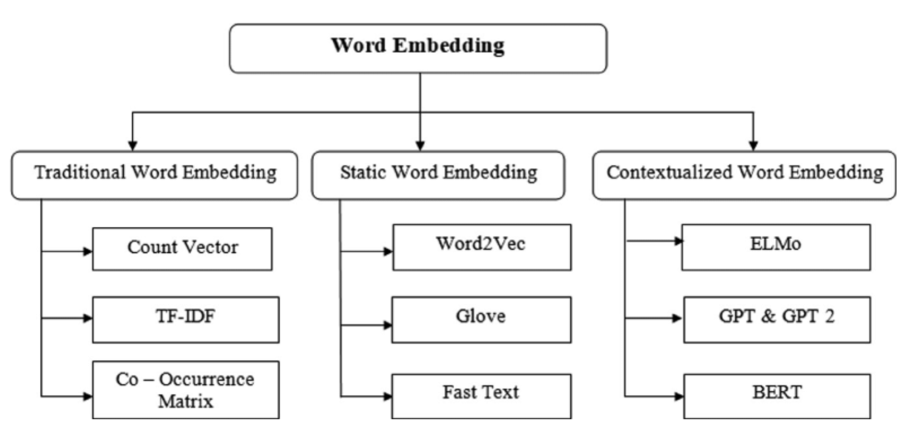
Large Language Model $\to$ ChatGPT

Datasets for pretraining stage

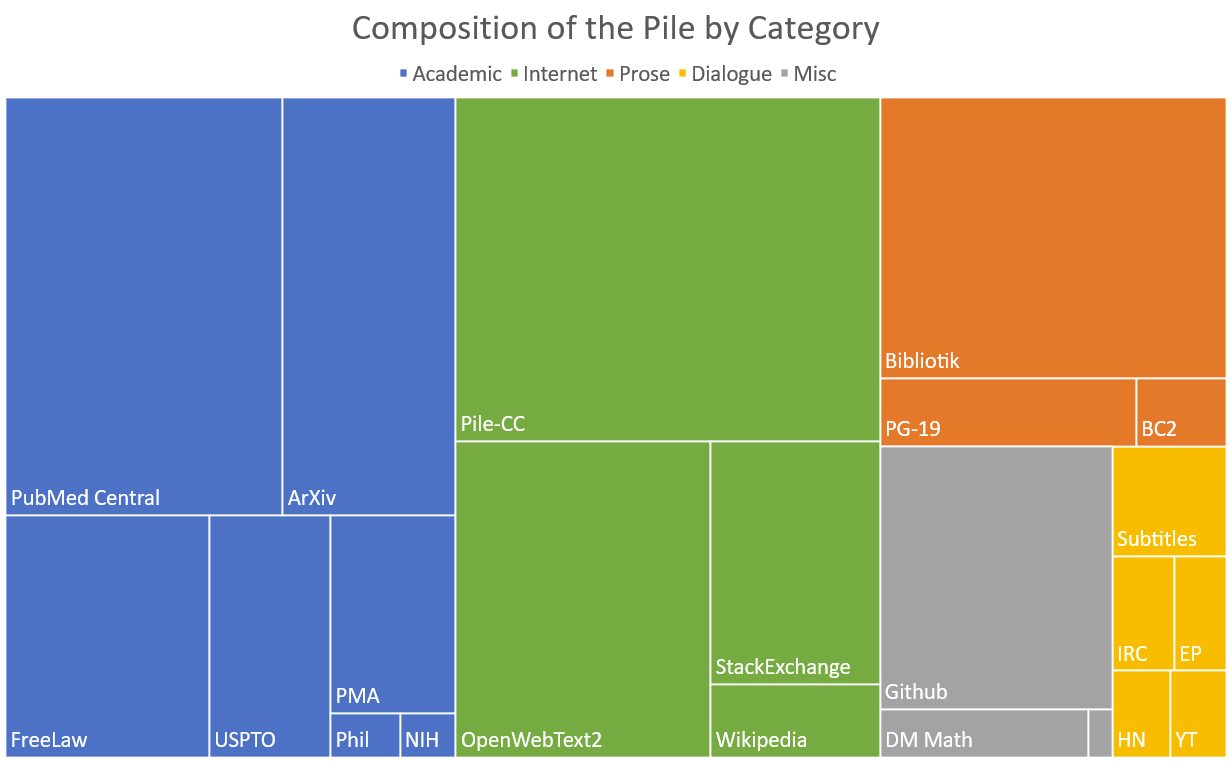
Pretraining base LLMs involves training on massive and diverse text datasets to capture a wide range of linguistic patterns, knowledge, and contextual understanding.

Common Crawl: A vast dataset of web pages, capturing diverse topics and writing styles
Wikipedia: A comprehensive and structured dataset of human knowledge across various domains
BooksCorpus: A dataset of published books offering rich narrative structures and varied vocabulary
OpenWebText: A curated dataset of high-quality web content similar to Reddit discussions
...

Perplexity in LLMs

In the context of language models, is defined as the exponential of the average log-likelihood per word in a given test set.

It can be interpreted as the weighted average number of choices a model has when predicting the next item in a sequence. A lower perplexity score indicates a better predictive model because it suggests the model has fewer choices, hence less uncertainty.

\[ P(W) = \exp\left(-\frac{1}{N} \sum_{i=1}^{N} \log p(w_i | w_1, \dots, w_{i-1})\right) \]

Perplexity evaluates the model's uncertainty in predicting the next word
High perplexity suggests the model is less certain and might be guessing among many options

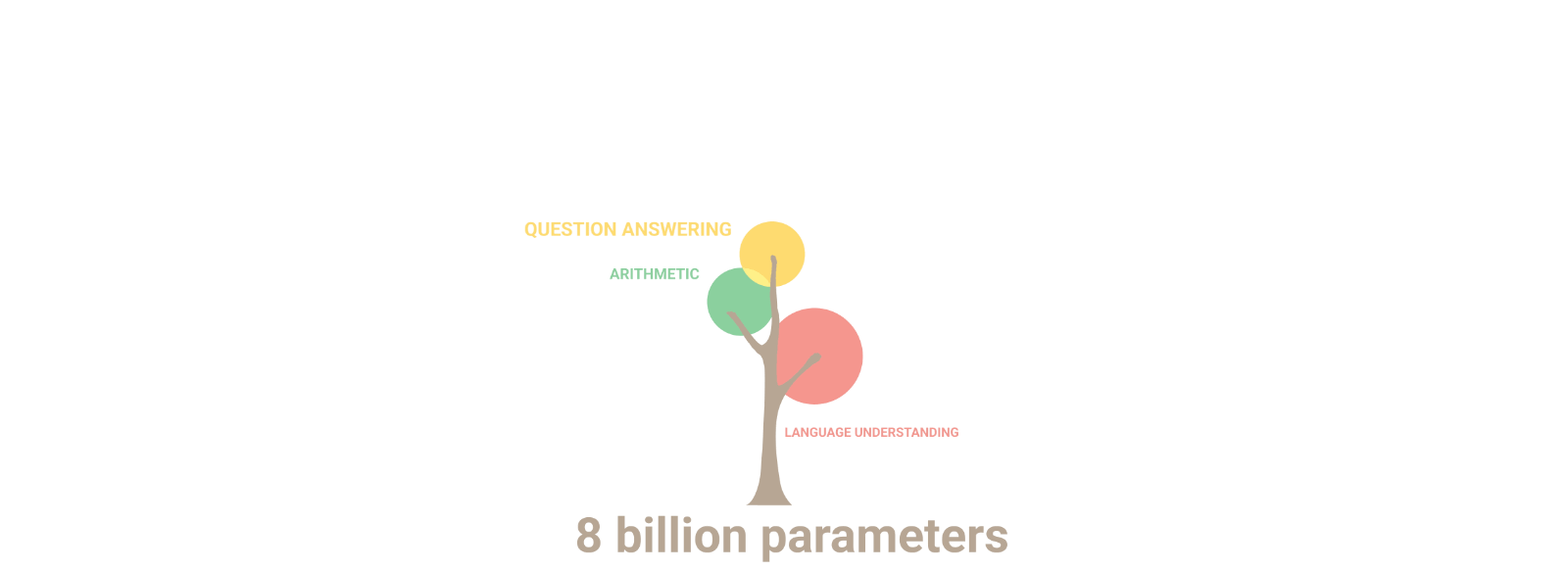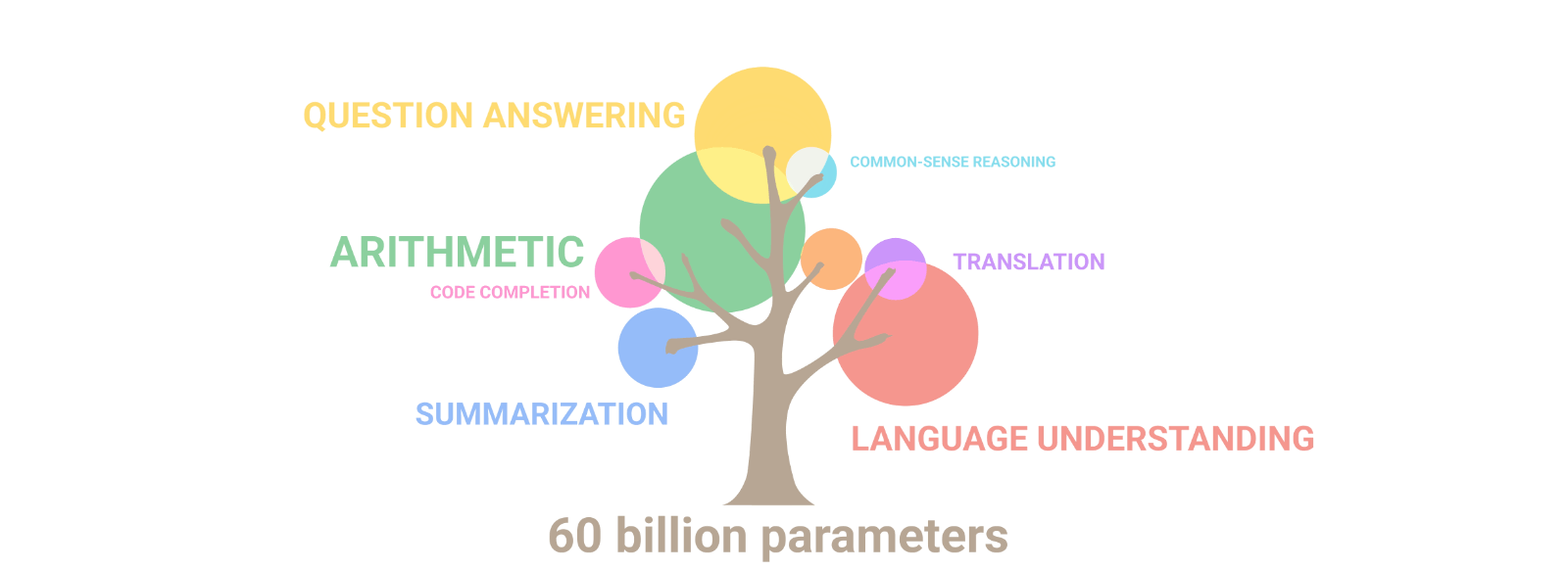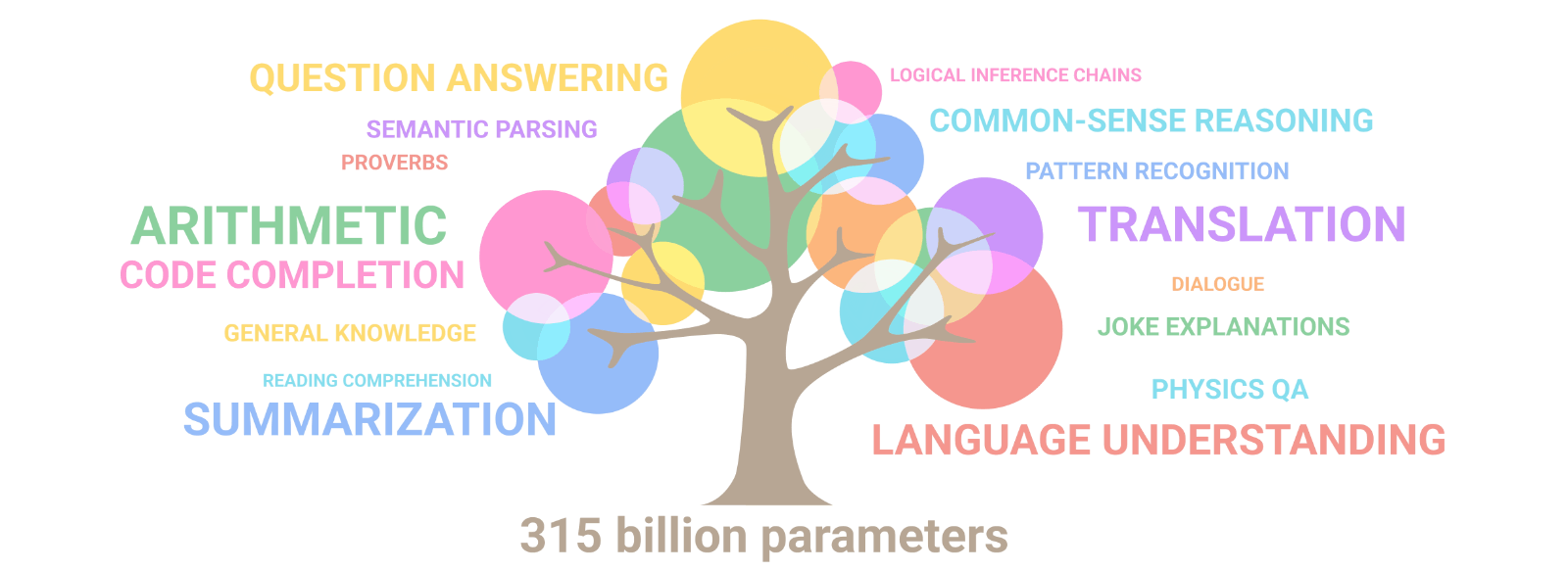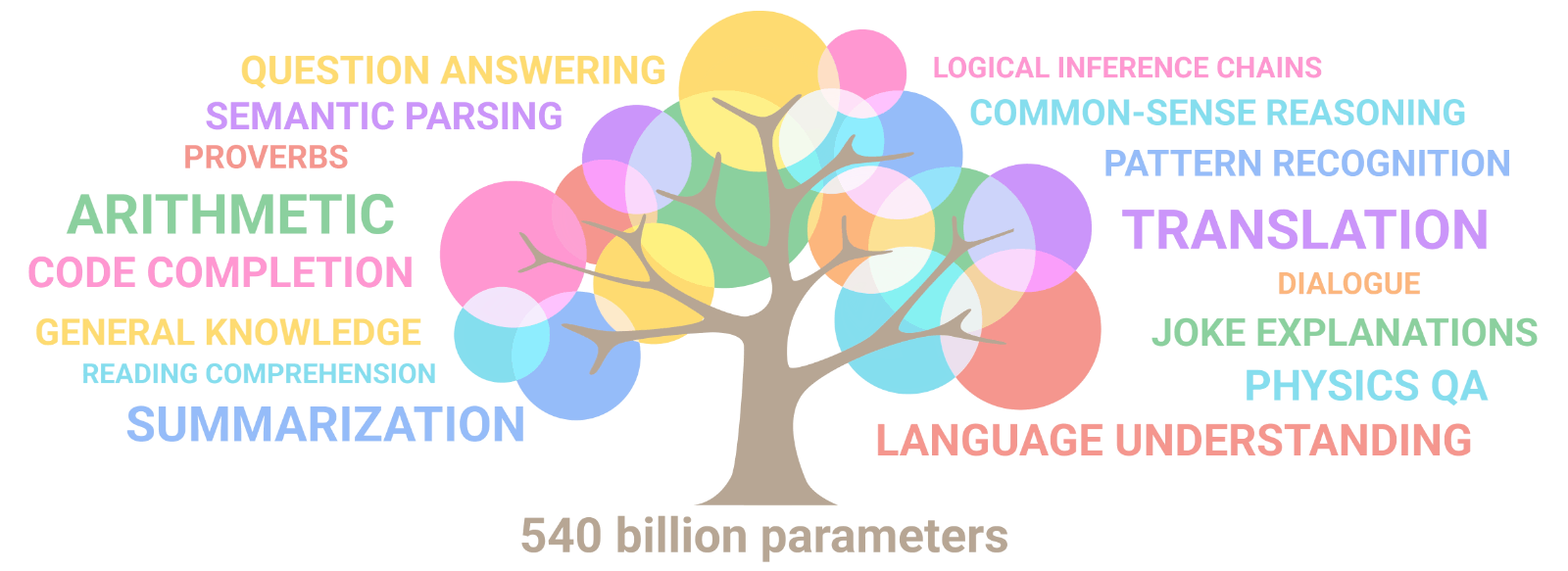
Unexpected abilities begin to emerge

Summary

Word Representation: Traditional methods like WordNet have limitations. Approaches like Word2Vec, CBOW, Skip-gram, and GloVe effectively capture semantic relationships.
Language Models: Large language models (LLMs) like BERT and GPT are trained on diverse datasets. Perplexity is one of the key metrics for evaluating their predictive performance.
Emergent Abilities: As LLMs scale, they exhibit unexpected capabilities, enhancing their utility in various NLP tasks.

What else can you explore?

Stanford class cs224n: lecture09 pretraining